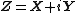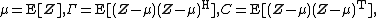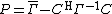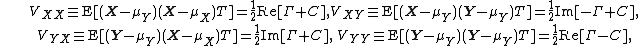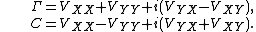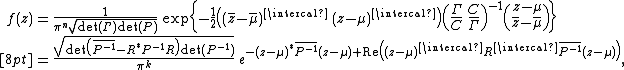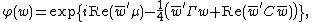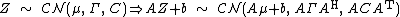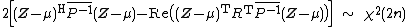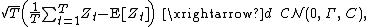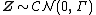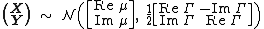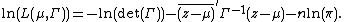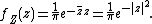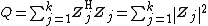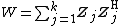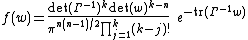“Complex normal distribution”的意思、由来-开放百科全书

词条

Complex normal distribution

释义

Definitions
Complex standard normal random variable Complex normal random variable Complex standard normal random vector Complex normal random vector
Notation
Mean and covariance
Relationships between covariance matrices
Density function
Characteristic function
Properties
Circularly-symmetric normal distribution
Definition Distribution of real and imaginary parts Probability density function Properties
See also
References
Further reading

{{Probability distribution
| name = Complex normal
| type = multivariate
| pdf_image =
| cdf_image =
| notation =
| parameters =

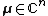— location

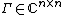— covariance matrix (positive semi-definite matrix)

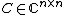— relation matrix (positive semi-definite matrix)

| support =

| pdf = complicated, see text
| mean =

| mode =

| variance =

| cf =

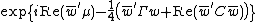
In probability theory, the family of complex normal distributions characterizes complex random variables whose real and imaginary parts are jointly normal.^[1] The complex normal family has three parameters: location parameter μ, covariance matrix , and the relation matrix . The standard complex normal is the univariate distribution with , , 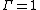and .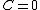

An important subclass of complex normal family is called the circularly-symmetric complex normal and corresponds to the case of zero relation matrix and zero mean: and 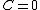.^[2] Circular symmetric complex normal random variables are used extensively in signal processing, and are sometimes referred to as just complex normal in signal processing literature.

Definitions

Complex standard normal random variable

The standard complex normal random variable or standard complex Gaussian random variable is a complex random variable whose real and imaginary parts are independent normally distributed random variables with mean zero and variance 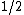.^[3]{{rp|p. 494}}^[4]{{rp|pp. 501}} Formally,

{{Equation box 1
|indent =
|title=
|equation = {{NumBlk||

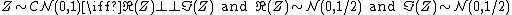|{{EquationRef|Eq.1}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}

where 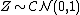denotes that is a standard complex normal random variable.

Complex normal random variable

Suppose and are real random variables such that is a 2-dimensional normal random vector. Then the complex random variable 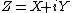is called complex normal random variable or complex Gaussian random variable.^[3]{{rp|p. 500}}

{{Equation box 1
|indent =
|title=
|equation = {{NumBlk||

|{{EquationRef|Eq.2}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}

Complex standard normal random vector

A n-dimensional complex random vector 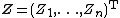is a complex standard normal random vector or complex standard Gaussian random vector if its components are independent and all of them are standard complex normal random variables as defined above.^[3]{{rp|p. 502}}^[4]{{rp|pp. 501}}

That is a standard complex normal random vector is denoted .

{{Equation box 1
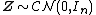|indent =
|title=
|equation = {{NumBlk||

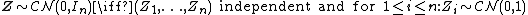|{{EquationRef|Eq.3}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}

Complex normal random vector

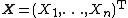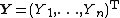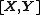If and are random vectors in such that is a normal random vector with components. Then we say that the complex random vector

has the is a complex normal random vector or a complex Gaussian random vector.

{{Equation box 1
|indent =
|title=
|equation = {{NumBlk||

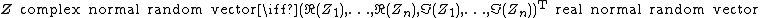|{{EquationRef|Eq.4}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}

Notation

The symbol 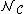is also used for the complex normal distribution.

Mean and covariance

The complex Gaussian distribution can be described with 3 parameters:^[5]

where 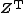denotes matrix transpose of , and 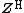denotes conjugate transpose.^[3]{{rp|p. 504}}^[4]{{rp|pp. 500}}

Here the location parameter is a n-dimensional complex vector; the covariance matrix is Hermitian and non-negative definite; and, the relation matrix or pseudo-covariance matrix is symmetric. The complex normal random vector 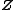can now be denoted as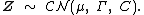Moreover, matrices and are such that the matrix

is also non-negative definite where 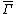denotes the complex conjugate of .^[5]

Relationships between covariance matrices

{{main|Complex random vector#Covariance matrix and pseudo-covariance matrix}}

As for any complex randm vector, the matrices and can be related to the covariance matrices of 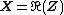and 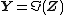via expressions

and conversely

Density function

The probability density function for complex normal distribution can be computed as

where 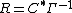and .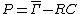

Characteristic function

The characteristic function of complex normal distribution is given by ^[5]

where the argument is a n-dimensional complex vector.

Properties

If is a complex normal n-vector, an m×n matrix, and a constant m-vector, then the linear transform 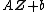will be distributed also complex-normally:

If is a complex normal n-vector, then

Central limit theorem. If 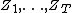are independent and identically distributed complex random variables, then

where and .

The modulus of a complex normal random variable follows a Hoyt distribution.^[6]

Circularly-symmetric normal distribution

Definition

A complex random vector is called circularly symmetric if for every deterministic 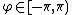the distribution of 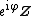equals the distribution of .^[4]{{rp|pp. 500–501}}.

Gaussian complex random vectors that are circularly symmetric are of particular interest because they are fully specified by the correlation matrix .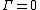

The 'circularly-symmetric normal distribution corresponds to the case of zero mean and zero relation matrix, i.e. and 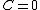^[3]{{rp|p. 507}}^[7]. This is usually denoted

Distribution of real and imaginary parts

If 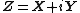is circularly-symmetric complex normal, then the vector 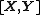is multivariate normal with covariance structure

where 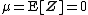and .

Probability density function

For nonsingular covariance matrix ,its distribution can also be simplified as^[3]{{rp|p. 508}}

.

Therefore, if the non-zero mean and covariance matrix are unknown, a suitable log likelihood function for a single observation vector would be

The standard complex normal (defined in {{EquationNote|Eq.1}})corresponds to the distribution of a scalar random variable with , 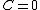and 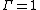. Thus, the standard complex normal distribution has density

Properties

The above expression demonstrates why the case 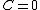, is called “circularly-symmetric”. The density function depends only on the magnitude of but not on its argument. As such, the magnitude 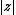of a standard complex normal random variable will have the Rayleigh distribution and the squared magnitude 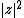will have the exponential distribution, whereas the argument will be distributed uniformly on .

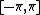If 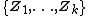are independent and identically distributed n-dimensional circular complex normal random vectors with , then the random squared norm

has the generalized chi-squared distribution and the random matrix

has the complex Wishart distribution with degrees of freedom. This distribution can be described by density function

where 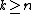, and is a nonnegative-definite matrix.

References

1. ^{{harvtxt|Goodman|1963}}
2. ^bookchapter, Gallager.R, pg9.
3. ^¹²³⁴⁵{{cite book | author=Lapidoth, A.| title=A Foundation in Digital Communication| publisher=Cambridge University Press | year=2009 | isbn=9780521193955}}
4. ^¹²³{{cite book |first=David |last=Tse |year=2005 |title=Fundamentals of Wireless Communication |publisher=Cambridge University Press}}
5. ^¹²{{harvtxt|Picinbono|1996}}
6. ^{{cite web |title=The Hoyt Distribution (Documentation for R package ‘shotGroups’ version 0.6.2) |author=Daniel Wollschlaeger |url=http://finzi.psych.upenn.edu/usr/share/doc/library/shotGroups/html/hoyt.html}}
7. ^bookchapter, Gallager.R

Definitions

Complex standard normal random variable

Complex normal random variable

Complex standard normal random vector

Complex normal random vector

Notation

Mean and covariance

Relationships between covariance matrices

Density function

Characteristic function

Properties

Circularly-symmetric normal distribution

Definition

Distribution of real and imaginary parts

Probability density function

Properties

See also

References

Further reading