“Computable analysis”的意思、由来-开放百科全书

词条

Computable analysis

释义

Basic constructions
Computable real numbers Computable real functions
Basic results
See also
References
External links

In mathematics and computer science, computable analysis is the study of mathematical analysis from the perspective of computability theory. It is concerned with the parts of real analysis and functional analysis that can be carried out in a computable manner. The field is closely related to constructive analysis and numerical analysis.

Basic constructions

Computable real numbers

Computable numbers are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm. They are also known as the recursive numbers or the computable reals.

Computable real functions

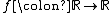A function is sequentially computable if, for every computable sequence of real numbers, the sequence is also computable.

Basic results

The computable real numbers form a real closed field (Weihrauch 2000, p. 180). The equality relation on computable real numbers is not computable, but for unequal computable real numbers the order relation is computable.

Computable real functions map computable real numbers to computable real numbers. The composition of computable real functions is again computable. Every computable real function is continuous (Weihrauch 2000, p. 6).

References

Oliver Aberth (1980), Computable analysis, McGraw-Hill, {{isbn|0-0700-0079-4}}.
Marian Pour-El and Ian Richards, Computability in Analysis and Physics, Springer-Verlag, 1989.
Stephen G. Simpson (1999), Subsystems of second-order arithmetic.
Klaus Weihrauch (2000), Computable analysis, Springer, {{isbn|3-540-66817-9}}.

External links

Computability and Complexity in Analysis Network

3 : Constructivism (mathematics)|Computability theory|Computable analysis

随便看