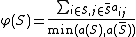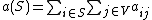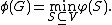“Conductance (graph)”的意思、由来-开放百科全书

词条

Conductance (graph)

释义

Generalizations and applications
Markov chains
See also
References

In graph theory the conductance of a graph G=(V,E) measures how "well-knit" the graph is: it controls how fast a random walk on G converges to a uniform distribution. The conductance of a graph is often called the Cheeger constant of a graph as the

analog of its counterpart in spectral geometry.{{fact|date=May 2010}} Since electrical networks are intimately related to random walks

with a long history in the usage of the term "conductance", this alternative name helps avoid possible confusion.

The conductance of a cut 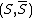in a graph is defined as:

where the are the entries of the adjacency matrix for G, so that

is the total number (or weight) of the edges incident with S. 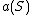is also called a volume of the set .

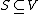The conductance of the whole graph is the minimum conductance over all the possible cuts:

Equivalently, conductance of a graph is defined as follows:

For a d-regular graph, the conductance is equal to the isoperimetric number divided by d.

Generalizations and applications

In practical applications, one often considers the conductance only over a cut. A common generalization of conductance is to handle the case of weights assigned to the edges: then the weights are added; if the weight is in the form of a resistance, then the reciprocal weights are added.

The notion of conductance underpins the study of percolation in physics and other applied areas; thus, for example, the permeability of petroleum through porous rock can be modeled in terms of the conductance of a graph, with weights given by pore sizes.

Conductance also helps measure the quality of a Spectral clustering. The maximum among the conductance of clusters provides a bound which can be used, along with inter-cluster edge weight, to define a measure on the quality of clustering. Intuitively, the conductance of a cluster(which can be seen as a set of vertices in a graph) should be low. Apart from this, the conductance of the subgraph induced by a cluster(called "internal conductance") can be used as well.

Markov chains

For an ergodic reversible Markov chain with an underlying graph G, the conductance is a way to measure how hard it is to leave a small set of nodes. Formally, the conductance of a graph is defined as the minimum over all sets of the capacity of divided by the ergodic flow out of . Alistair Sinclair showed that conductance is closely tied to mixing time in ergodic reversible Markov chains. We can also view conductance in a more probabilistic way, as the minimal probability of leaving a small set of nodes given that we started in that set to begin with. Writing 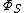for the conditional probability of leaving a set of nodes S given that we were in that set to begin with, the conductance is the minimal 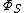over sets that have a total stationary probability of at most 1/2.

Conductance is related to Markov chain mixing time in the reversible setting.

References

{{cite book | author=Béla Bollobás | authorlink=Béla Bollobás | title=Modern graph theory | series=GTM | volume=184 | publisher=Springer-Verlag | date=1998 | isbn=0-387-98488-7 | page=321 }}
{{cite journal | url=http://www.cc.gatech.edu/~vempala/papers/jacm-spectral.pdf | author=Kannan, R. |author2=Vempala, S. |author3=Vetta, A. | date=May 2004 | title=On clusterings: Good, bad and spectral | journal=J. ACM |volume= 51 | issue =3 | pages=497–515 | doi = 10.1145/990308.990313 }}
{{cite book | author=Fan Chung | authorlink = Fan Chung | title=Spectral Graph Theory | series=CBMS Lecture Notes | volume=92 | publisher=AMS Publications | date=1997 | isbn=0-8218-0315-8 | page=212}}
A. Sinclair. Algorithms for Random Generation and Counting: A Markov Chain Approach. Birkhauser, Boston-Basel-Berlin, 1993.
D. Levin, Y. Peres, E. L. Wilmer: Markov Chains and Mixing Times

4 : Markov processes|Algebraic graph theory|Matrices|Graph invariants

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Generalizations and applications

Markov chains

See also

References