“Contiguity (probability theory)”的意思、由来-开放百科全书

词条

Contiguity (probability theory)

释义

Definition
Applications
See also
Notes
References
Additional literature
External links

In probability theory, two sequences of probability measures are said to be contiguous if asymptotically they share the same support. Thus the notion of contiguity extends the concept of absolute continuity to the sequences of measures.

The concept was originally introduced by {{harvtxt|Le Cam|1960}} as part of his contribution to the development of abstract general asymptotic theory in mathematical statistics. Le Cam was instrumental during the period in the development of abstract general asymptotic theory in mathematical statistics. He is best known for the general concepts of local asymptotic normality and contiguity.^[1]

Definition

Let 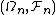be a sequence of measurable spaces, each equipped with two measures P_n and Q_n.

We say that Q_n is contiguous with respect to P_n (denoted {{nowrap|Q_n ◁ P_n}}) if for every sequence A_n of measurable sets, {{nowrap|P_n(A_n) → 0}} implies {{nowrap|Q_n(A_n) → 0}}.
The sequences P_n and Q_n are said to be mutually contiguous or bi-contiguous (denoted {{nowrap|Q_n ◁▷ P_n}}) if both Q_n is contiguous with respect to P_n and P_n is contiguous with respect to Q_n.^[2]

The notion of contiguity is closely related to that of absolute continuity. We say that a measure Q is absolutely continuous with respect to P (denoted {{nowrap|Q ≪ P}}) if for any measurable set A, {{nowrap|1 = P(A) = 0}} implies {{nowrap|1 = Q(A) = 0}}. That is, Q is absolutely continuous with respect to P if the support of Q is a subset of the support of P, except in cases where this is false, including, e.g., a measure that concentrates on an open set, because its support is a closed set and it assigns measure zero to the boundary, and so another measure may concentrate on the boundary and thus have support contained within the support of the first measure, but they will be mutually singular. In summary, this previous sentence's statement of absolute continuity is false. The contiguity property replaces this requirement with an asymptotic one: Q_n is contiguous with respect to P_n if the "limiting support" of Q_n is a subset of the limiting support of P_n. By the aforementioned logic, this statement is also false.

It is possible however that each of the measures Q_n be absolutely continuous with respect to P_n, while the sequence Q_n not being contiguous with respect to P_n.

The fundamental Radon–Nikodym theorem for absolutely continuous measures states that if Q is absolutely continuous with respect to P, then Q has density with respect to P, denoted as {{nowrap|1=ƒ = {{frac|dQ|dP}}}}, such that for any measurable set A

which is interpreted as being able to "reconstruct" the measure Q from knowing the measure P and the derivative ƒ. A similar result exists for contiguous sequences of measures, and is given by the Le Cam's third lemma.

Applications

Econometrics ^[3]

Notes

1. ^Wolfowitz J.(1974) Review of the book: "Contiguity of Probability Measures: Some Applications in Statistics. by George G. Roussas",Journal of the American Statistical Association, 69, 278–279 [https://www.jstor.org/pss/2285551 jstor]
2. ^{{harvtxt|van der Vaart|1998|page=87}}
3. ^{{cite web |url=http://www.samsi.info/200506/fmse/course-info/werker-updated-nov14.pdf |title=Archived copy |accessdate=2009-11-12 |deadurl=yes |archiveurl=https://web.archive.org/web/20081011185612/http://www.samsi.info/200506/fmse/course-info/werker-updated-nov14.pdf |archivedate=2008-10-11 |df= }}

References

{{cite book

{{cite journal

{{SpringerEOM

| last = Roussas
| first = George G.
| title = Contiguity of probability measures
| id = C/c120210

{{cite book

| last = van der Vaart
| first = A. W.
| title = Asymptotic statistics
| year = 1998
| publisher = Cambridge University Press
| ref = CITEREFvan_der_Vaart1998{{refend}}

Additional literature

Roussas, George G. (1972), Contiguity of Probability Measures: Some Applications in Statistics, CUP, {{ISBN|978-0-521-09095-7}}.
Scott, D.J. (1982) Contiguity of Probability Measures, Australian & New Zealand Journal of Statistics, 24 (1), 80–88.

External links

Contiguity Asymptopia: 17 October 2000, David Pollard
Asymptotic normality under contiguity in a dependence case
A Central Limit Theorem under Contiguous Alternatives
Superefficiency, Contiguity, LAN, Regularity, Convolution Theorems
[https://books.google.com/books?id=IlJE_9_e8UEC&pg=PA493&lpg=PA493&dq=Contiguity+space+asymptotic+normality&source=bl&ots=PAaWWTDYs6&sig=OoQ02c_PCTpaj3olElV6M-TV8qM&hl=en&ei=aohrSsqODJCiswOQs5iXBQ&sa=X&oi=book_result&ct=result&resnum=6 Testing statistical hypotheses]
Necessary and sufficient conditions for contiguity and entire asymptotic separation of probability measures R Sh Liptser et al 1982 Russ. Math. Surv. 37 107–136
[https://books.google.com/books?id=ifUA5CBiQ44C&pg=PA324&lpg=PA324&dq=%22Contiguity+space%22&source=bl&ots=6sgYRZGaz7&sig=Fd7FL3vexvpesM7NXS15qKcUJOk&hl=en&ei=6YBrSsT3D5TUsQOItpmXBQ&sa=X&oi=book_result&ct=result&resnum=1 The unconscious as infinite sets By Ignacio Matte Blanco, Eric (FRW) Rayner]
[https://archive.today/20130105172921/http://www3.interscience.wiley.com/journal/119856597/abstract?CRETRY=1&SRETRY=0 "Contiguity of Probability Measures", David J. Scott, La Trobe University]
[https://www.jstor.org/pss/2242899 "On the Concept of Contiguity", Hall, Loynes]

1 : Probability theory

随便看