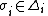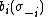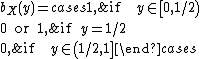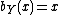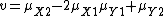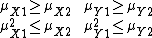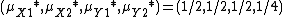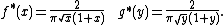请输入您要查询的百科知识：

　

词条 Continuous game
释义

  1. Formal definition

     Separable games 

  2. Examples

     Separable games  A polynomial game  Non-Separable Games  A rational pay-off function  Requiring a Cantor distribution 

  3. Further reading

  4. See also

  5. References

{{Refimprove|date=March 2009}}

A continuous game is a mathematical concept, used in game theory, that generalizes the idea of an ordinary game like tic-tac-toe (noughts and crosses) or checkers (draughts). In other words, it extends the notion of a discrete game, where the players choose from a finite set of pure strategies. The continuous game concepts allows games to include more general sets of pure strategies, which may be uncountably infinite.

In general, a game with uncountably infinite strategy sets will not necessarily have a Nash equilibrium solution. If, however, the strategy sets are required to be compact and the utility functions continuous, then a Nash equilibrium will be guaranteed; this is by Glicksberg's generalization of the Kakutani fixed point theorem. The class of continuous games is for this reason usually defined and studied as a subset of the larger class of infinite games (i.e. games with infinite strategy sets) in which the strategy sets are compact and the utility functions continuous.

Formal definition

Define the n-player continuous gam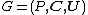e where

is the set of players,

where each is a compact metric space corresponding to the th player's set of pure strategies,

where is the utility function of player

We define to be the set of Borel probability measures on , giving us the mixed strategy space of player i.

Define the strategy profile where

Let 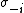be a strategy profile of all players except for player . As with discrete games, we can define a best response correspondence for player , 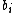. 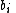is a relation from the set of all probability distributions over opponent player profiles to a set of player 's strategies, such that each element of

is a best response to . Define

.

A strategy profile 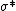is a Nash equilibrium if and only if

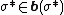
The existence of a Nash equilibrium for any continuous game with continuous utility functions can be proven using Irving Glicksberg's generalization of the Kakutani fixed point theorem.[1] In general, there may not be a solution if we allow strategy spaces, 's which are not compact, or if we allow non-continuous utility functions.

Separable games

A separable game is a continuous game where, for any i, the utility function 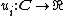can be expressed in the sum-of-products form:

, where , , , and the functions are continuous.

A polynomial game is a separable game where each is a compact interval on 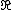and each utility function can be written as a multivariate polynomial.

In general, mixed Nash equilibria of separable games are easier to compute than non-separable games as implied by the following theorem:

For any separable game there exists at least one Nash equilibrium where player i mixes at most pure strategies.[2]

Whereas an equilibrium strategy for a non-separable game may require an uncountably infinite support, a separable game is guaranteed to have at least one Nash equilibrium with finitely supported mixed strategies.

Examples

Separable games

A polynomial game

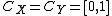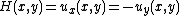Consider a zero-sum 2-player game between players X and Y, with . Denote elements of and as and respectively. Define the utility functions where

.

The pure strategy best response relations are:

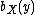and 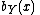do not intersect, so there is

no pure strategy Nash equilibrium.

However, there should be a mixed strategy equilibrium. To find it, express the expected value, 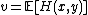as a linear combination of the first and second moments of the probability distributions of X and Y:

(where 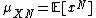and similarly for Y).

The constraints on 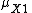and 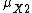(with similar constraints for y,) are given by Hausdorff as:

Each pair of constraints defines a compact convex subset in the plane. Since is linear, any extrema with respect to a player's first two moments will lie on the boundary of this subset. Player i's equilibrium strategy will lie on

Note that the first equation only permits mixtures of 0 and 1 whereas the second equation only permits pure strategies. Moreover, if the best response at a certain point to player i lies on 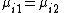, it will lie on the whole line, so that both 0 and 1 are a best response. 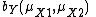simply gives the pure strategy 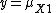, so 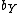will never give both 0 and 1.

However gives both 0 and 1 when y = 1/2.

A Nash equilibrium exists when:

This determines one unique equilibrium where Player X plays a random mixture of 0 for 1/2 of the time and 1 the other 1/2 of the time. Player Y plays the pure strategy of 1/2. The value of the game is 1/4.

Non-Separable Games

A rational pay-off function

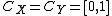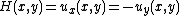Consider a zero-sum 2-player game between players X and Y, with . Denote elements of and as and respectively. Define the utility functions where

This game has no pure strategy Nash equilibrium. It can be shown[3] that a unique mixed strategy Nash equilibrium exists with the following pair of probability density functions:

The value of the game is .

Requiring a Cantor distribution

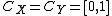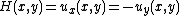Consider a zero-sum 2-player game between players X and Y, with . Denote elements of and as and respectively. Define the utility functions where

.

This game has a unique mixed strategy equilibrium where each player plays a mixed strategy with the cantor singular function as the cumulative distribution function.[4]

Further reading

  • H. W. Kuhn and A. W. Tucker, eds. (1950). Contributions to the Theory of Games: Vol. II. Annals of Mathematics Studies 28. Princeton University Press. {{ISBN|0-691-07935-8}}.

See also

  • Graph continuous

References

1. ^I.L. Glicksberg. A further generalization of the Kakutani fixed point theorem, with application to Nash equilibrium points. Proceedings of the American Mathematical Society, 3(1):170–174, February 1952.
2. ^N. Stein, A. Ozdaglar and P.A. Parrilo. "Separable and Low-Rank Continuous Games". International Journal of Game Theory, 37(4):475–504, December 2008. https://arxiv.org/abs/0707.3462
3. ^Glicksberg, I. & Gross, O. (1950). "Notes on Games over the Square." Kuhn, H.W. & Tucker, A.W. eds. Contributions to the Theory of Games: Volume II. Annals of Mathematics Studies 28, p.173–183. Princeton University Press.
4. ^Gross, O. (1952). "A rational payoff characterization of the Cantor distribution." TechnicalReport D-1349, The RAND Corporation.

1 : Game theory game classes
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 0:19:14