请输入您要查询的百科知识：

　

词条 Convex volume approximation
释义

  1. References

In the analysis of algorithms, several authors have studied the computation of the volume of high-dimensional convex bodies, a problem that can also be used to model many other problems in combinatorial enumeration.

Often these works use a black box model of computation in which the input is given by a subroutine for testing whether a point is inside or outside of the convex body, rather than by an explicit listing of the vertices or faces of a convex polytope.

It is known that, in this model, no deterministic algorithm can achieve an accurate approximation,{{R|E|BF}} and even for an explicit listing of faces or vertices the problem is #P-hard.{{r|DF}}

However, a joint work by Martin Dyer, Alan M. Frieze and Ravindran Kannan provided a randomized polynomial time approximation scheme for the problem,

providing a sharp contrast between the capabilities of randomized and deterministic algorithms.{{r|DFK}}

The main result of the paper is a randomized algorithm for finding an approximation to the volume of a convex body in -dimensional Euclidean space by assuming the existence of a membership oracle. The algorithm takes time bounded by a polynomial in , the dimension of and .

The algorithm combines two ideas:

  • By using a Markov chain Monte Carlo (MCMC) method, it is possible to generate points that are nearly uniformly randomly distributed within a given convex body. The basic scheme of the algorithm is a nearly uniform sampling from within by placing a grid consisting of -dimensional cubes and doing a random walk over these cubes. By using the theory of rapidly mixing Markov chains, they show that it takes a polynomial time for the random walk to settle down to being a nearly uniform distribution.{{r|DFK}}
  • By using rejection sampling, it is possible to compare the volumes of two convex bodies, one nested within another, when their volumes are within a small factor of each other. The basic idea is to generate random points within the outer of the two bodies, and to count how often those points are also within the inner body.

The given convex body can be approximated by a sequence of nested bodies, eventually reaching one of known volume (a hypersphere), with this approach used to estimate the factor by which the volume changes at each step of this sequence. Multiplying these factors gives the approximate volume of the original body.

This work earned its authors the 1991 Fulkerson Prize.[1]

Although the time for this algorithm is polynomial, it has a high exponent.

Subsequent authors improved the running time of this method by providing more quickly mixing Markov chains for the same problem.{{r|AK|KLS|LS|LV}}

References

1. ^Fulkerson Prize winners, American Mathematical Society, retrieved 2017-08-03.
2. ^{{citation | last1 = Bárány | first1 = Imre | author1-link = Imre Bárány | last2 = Füredi | first2 = Zoltán | author2-link = Zoltán Füredi | doi = 10.1007/BF02187886 | issue = 4 | journal = Discrete and Computational Geometry | mr = 911186 | pages = 319–326 | title = Computing the volume is difficult | volume = 2 | year = 1987}}
3. ^{{citation | last1 = Dyer | first1 = Martin | author1-link = Martin Dyer | last2 = Frieze | first2 = Alan | author2-link = Alan M. Frieze | doi = 10.1137/0217060 | issue = 5 | journal = SIAM Journal on Computing | mr = 961051 | pages = 967–974 | title = On the complexity of computing the volume of a polyhedron | volume = 17 | year = 1988}}
4. ^{{citation | last1 = Dyer | first1 = Martin | author1-link = Martin Dyer | last2 = Frieze | first2 = Alan | author2-link = Alan M. Frieze | last3 = Kannan | first3 = Ravi | author3-link = Ravindran Kannan | doi = 10.1145/102782.102783 | issue = 1 | journal = Journal of the ACM | mr = 1095916 | pages = 1–17 | title = A random polynomial-time algorithm for approximating the volume of convex bodies | volume = 38 | year = 1991}}
5. ^{{citation | last = Elekes | first = G. | authorlink = György Elekes | doi = 10.1007/BF02187701 | issue = 4 | journal = Discrete and Computational Geometry | mr = 866364 | pages = 289–292 | title = A geometric inequality and the complexity of computing volume | volume = 1 | year = 1986}}
6. ^{{citation | last1 = Kannan | first1 = Ravi | author1-link = Ravindran Kannan | last2 = Lovász | first2 = László | author2-link = László Lovász | last3 = Simonovits | first3 = Miklós | author3-link = Miklós Simonovits | doi = 10.1002/(SICI)1098-2418(199708)11:1<1::AID-RSA1>3.0.CO;2-X | issue = 1 | journal = Random Structures & Algorithms | mr = 1608200 | pages = 1–50 | title = Random walks and an 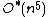volume algorithm for convex bodies | volume = 11 | year = 1997}}
7. ^{{citation | last1 = Lovász | first1 = L. | author1-link = László Lovász | last2 = Simonovits | first2 = M. | author2-link = Miklós Simonovits | doi = 10.1002/rsa.3240040402 | issue = 4 | journal = Random Structures & Algorithms | mr = 1238906 | pages = 359–412 | title = Random walks in a convex body and an improved volume algorithm | volume = 4 | year = 1993}}
8. ^{{citation | last1 = Lovász | first1 = L. | author1-link = László Lovász | last2 = Vempala | first2 = Santosh | author2-link = Santosh Vempala | doi = 10.1016/j.jcss.2005.08.004 | issue = 2 | journal = Journal of Computer and System Sciences | mr = 2205290 | pages = 392–417 | title = Simulated annealing in convex bodies and an 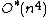volume algorithm | volume = 72 | year = 2006}}
[2][3][4][5][6][7][8]
}}

2 : Computational geometry|Approximation algorithms
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/13 8:00:37