“Cornacchia's algorithm”的意思、由来-开放百科全书

词条

Cornacchia's algorithm

释义

The algorithm
Example
References
External links

In computational number theory, Cornacchia's algorithm is an algorithm for solving the Diophantine equation , where and d and m are coprime. The algorithm was described in 1908 by Giuseppe Cornacchia.^[1]

The algorithm

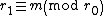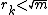First, find any solution to (perhaps by using an algorithm listed here); if no such exist, there can be no primitive solution to the original equation. Without loss of generality, we can assume that {{math|r₀ ≤ {{sfrac|m|2}}}} (if not, then replace {{math|r₀}} with {{math| m - r₀}}, which will still be a root of {{math|-d}}). Then use the Euclidean algorithm to find , and so on; stop when . If 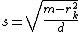is an integer, then the solution is 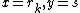; otherwise there is no primitive solution.

To find non-primitive solutions {{math|(x, y)}} where {{math| gcd(x, y) {{=}} g ≠ 1}}, note that the existence of such a solution implies that {{math|g²}} divides {{mvar|m}} (and equivalently, that if {{mvar|m}} is square-free, then all solutions are primitive). Thus the above algorithm can be used to search for a primitive solution {{math|(u, v)}} to {{math| u² + dv² {{=}} {{sfrac|m|g²}}}}. If such a solution is found, then {{math|(gu, gv)}} will be a solution to the original equation.

Example

Solve the equation . A square root of −6 (mod 103) is 32, and 103 ≡ 7 (mod 32); since 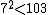and 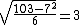, there is a solution x = 7, y = 3.

References

1. ^{{cite journal|last=Cornacchia|first=G.|year=1908|title=Su di un metodo per la risoluzione in numeri interi dell' equazione

.|journal=Giornale di Matematiche di Battaglini|volume=46|pages=33–90}}

External links

{{cite journal|url=http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.pja/1116442240|title=On the solutions of |last=Basilla|first=J. M. |journal=Proc. Japan Acad. |volume=80(A) |year=2004 |pages=40-41 |format=PDF}}

1 : Number theoretic algorithms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。