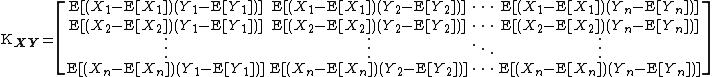“Cross-covariance matrix”的意思、由来-开放百科全书

词条

Cross-covariance matrix

释义

Definition
Example
Properties
Definition for complex random vectors
Uncorrelatedness
References

In probability theory and statistics, a cross-covariance matrix is a matrix whose element in the i, j position is the covariance between the i-th element of a random vector and j-th element of another random vector. A random vector is a random variable with multiple dimensions. Each element of the vector is a scalar random variable. Each element has either a finite number of observed empirical values or a finite or infinite number of potential values. The potential values are specified by a theoretical joint probability distribution. Intuitively, the cross-covariance matrix generalizes the notion of covariance to multiple dimensions.

The cross-covariance matrix of two random vectors and 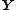is typically denoted by or .

Definition

For random vectors and 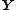, each containing random elements whose expected value and variance exist, the cross-covariance matrix of and 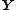is defined by^[1]{{rp|p.336}}

{{Equation box 1
|indent =
|title=
|equation = {{NumBlk||

|{{EquationRef|Eq.1}}}}
|cellpadding= 6
|border
|border colour = #0073CF
|background colour=#F5FFFA}}

where and are vectors containing the expected values of and 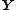. The vectors and 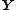need not have the same dimension, and either might be a scalar value.

The cross-covariance matrix is the matrix whose entry is the covariance

between the i-th element of and the j-th element of 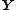. This gives the following component-wise definition of the cross-covariance matrix.

Example

For example, if and are random vectors, then

is a matrix whose -th entry is .

Properties

For the cross-covariance matrix, the following basic properties apply:^[2]

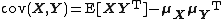
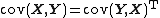
If and 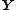are independent (or somewhat less restrictedly, if every random variable in is uncorrelated with every random variable in 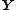), then

where , 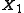and are random 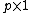vectors, 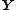is a random vector, is a vector, is a 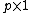vector, and are matrices of constants, and is a matrix of zeroes.

Definition for complex random vectors

{{Main|Complex random vector#Cross-covariance matrix and pseudo-cross-covariance matrix}}

If and are complex random vectors, the definition of the cross-covariance matrix is slightly changed. Transposition is replaced by hermitan transposition:

For complex random vectors, another matrix called the pseudo-cross-covariance matrix is defined as follows:

Uncorrelatedness

Two random vectors and 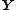are called uncorrelated if their cross-covariance matrix matrix is zero.^[3]{{rp|p.337}}

Complex random vectors and are called uncorrelated if their covariance matrix and pseudo-covariance matrix is zero, i.e. if .

References

1. ^{{cite book |first=John A. |last=Gubner |year=2006 |title=Probability and Random Processes for Electrical and Computer Engineers |publisher=Cambridge University Press |isbn=978-0-521-86470-1}}
2. ^{{cite web |last1=Taboga |first1=Marco |url=http://www.statlect.com/varian2.htm |title=Lectures on probability theory and mathematical statistics |year=2010}}
3. ^{{cite book |first=John A. |last=Gubner |year=2006 |title=Probability and Random Processes for Electrical and Computer Engineers |publisher=Cambridge University Press |isbn=978-0-521-86470-1}}

2 : Covariance and correlation|Matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。