“Crossing number (knot theory)”的意思、由来-开放百科全书

In the mathematical area of knot theory, the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant.

Examples

By way of example, the unknot has crossing number zero, the trefoil knot three and the figure-eight knot four. There are no other knots with a crossing number this low, and just two knots have crossing number five, but the number of knots with a particular crossing number increases rapidly as the crossing number increases.

Tabulation

Tables of prime knots are traditionally indexed by crossing number, with a subscript to indicate which particular knot out of those with this many crossings is meant (this sub-ordering is not based on anything in particular, except that torus knots then twist knots are listed first). The listing goes 3₁ (the trefoil knot), 4₁ (the figure-eight knot), 5₁, 5₂, 6₁, etc. This order has not changed significantly since P. G. Tait published a tabulation of knots in 1877.^[1]

Additivity

There has been very little progress on understanding the behavior of crossing number under rudimentary operations on knots. A big open question asks if the crossing number is additive when taking knot sums. It is also expected that a satellite of a knot K should have larger crossing number than K, but this has not been proven.

Additivity of crossing number under knot sum has been proven for special cases, for example if the summands are alternating knots^[2] (or more generally, adequate knot), or if the summands are torus knots.^[3]^[4] Marc Lackenby has also given a proof that there is a constant N > 1 such that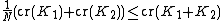

, but his method, which utilizes normal surfaces, cannot improve N to 1.^[5]

Applications in bioinformatics

There are connections between the crossing number of a knot and the physical behavior of DNA knots. For prime DNA knots, crossing number is a good predictor of the relative velocity of the DNA knot in agarose gel electrophoresis. Basically, the higher the crossing number, the faster the relative velocity. For composite knots, this does not appear to be the case, although experimental conditions can drastically change the results.^[6]

Related invariants

There are related concepts of average crossing number and asymptotic crossing number. Both of these quantities bound the standard crossing number. Asymptotic crossing number is conjectured to be equal to crossing number.

Other numerical knot invariants include the bridge number, linking number, stick number, and unknotting number.

References

1. ^{{citation|authorlink=P.G. Tait|last=Tait|first=P. G.|contribution=On Knots I,II,III'|title=Scientific papers|volume=1|pages=273–347|publisher=Cambridge University Press|year=1898}}.
2. ^{{citation|authorlink=Colin Adams (mathematician)|last=Adams|first=Colin C.|year=2004|title=The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots|mr=2079925|location=Providence, RI|publisher=American Mathematical Society|isbn= 9780821836781|page=69|url=https://books.google.com/books?id=M-B8XedeL9sC&pg=PA69}}.
3. ^{{citation|last=Gruber|first=H.|title=Estimates for the minimal crossing number|arxiv=math/0303273|year=2003|bibcode=2003math......3273G}}.
4. ^{{citation | last = Diao | first = Yuanan | doi = 10.1142/S0218216504003524 | issue = 7 | journal = Journal of Knot Theory and its Ramifications | mr = 2101230 | pages = 857–866 | title = The additivity of crossing numbers | volume = 13 | year = 2004}}.
5. ^{{citation | last = Lackenby | first = Marc | authorlink = Marc Lackenby | doi = 10.1112/jtopol/jtp028 | issue = 4 | journal = Journal of Topology | mr = 2574742 | pages = 747–768 | title = The crossing number of composite knots | url = http://www.maths.ox.ac.uk/~lackenby/csk16058.ps | volume = 2 | year = 2009| arxiv = 0805.4706 }}.
6. ^{{citation|contribution=Energy functions for knots: Beginning to predict physical behavior|title=Mathematical Approaches to Biomolecular Structure and Dynamics|series=The IMA Volumes in Mathematics and its Applications|volume=82|year=1996|pages=39–58|first=Jonathan|last=Simon|doi=10.1007/978-1-4612-4066-2_4|editor1-first=Jill P.|editor1-last=Mesirov|editor1-link=Jill P. Mesirov|editor2-first=Klaus|editor2-last=Schulten|editor3-first=De Witt|editor3-last=Sumners|editor3-link=De Witt Sumners}}.