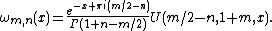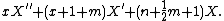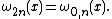- Notes
- References
In statistics, the Cunningham function or Pearson–Cunningham function ωm,n(x) is a generalisation of a special function introduced by {{harvtxt|Pearson|1906}} and studied in the form here by {{harvtxt|Cunningham|1908}}. It can be defined in terms of the confluent hypergeometric function U, by
The function was studied by Cunningham[1] in the context of a multivariate generalisation of the Edgeworth expansion for approximating a probability density function based on its (joint) moments. In a more general context, the function is related to the solution of the constant-coefficient diffusion equation, in one or more dimensions.[1]
The function ωm,n(x) is a solution of the differential equation for X:[1]
The special function studied by Pearson is given, in his notation by,[1]
Notes
References
- {{AS ref|13|510}}
- {{Citation | last1=Cunningham | first1=E. | title=The ω-Functions, a Class of Normal Functions Occurring in Statistics | jstor=93061 | publisher=The Royal Society | year=1908 | journal=Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character | issn=0950-1207 | volume=81 | issue=548 | pages=310–331 | doi=10.1098/rspa.1908.0085}}
- {{citation|first=Karl|last=Pearson|authorlink=Karl Pearson|title=A mathematical theory of random migration|publisher=London, Dulau and co.|year= 1906}}
- {{Citation | last1=Whittaker | first1=E. T. | last2=Watson | first2=G. N. | title=A Course in Modern Analysis | publisher=Cambridge University Press | isbn=978-0-521-58807-2 | year=1963 }} See exercise 10, chapter XVI, p. 353
- Balaguier-sur-Rance
- Balagund
- Balagundi
- Balagundi, Western Australia
- Balaguères
- Bala Gëyushlyu
- Bala Göyüşlü
- Balaha Kathal
- Balahar
- Balahasaghara
- Bala Hasanli
- Bala Hasimxanli
- Bala Haşimxanlı
- Bala Haşımxanlı
- Balahesar
- Bala Hesenli
- Bala Hisar
- Bala Hissar Fort
- Balahovit
- Balahtinski
- Balahtinski District
- Balahtinskii
- Balahtinskii District
- Balahtinskii Raion
- Balahtinski Raion