“Cycle decomposition (graph theory)”的意思、由来-开放百科全书

词条

Cycle decomposition (graph theory)

释义

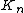Cycle decomposition of and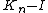
References

{{For|the notation used to express permutations|Cycle decomposition (group theory)}}

In graph theory, a cycle decomposition is a decomposition (a partitioning of a graph's edges) into cycles. Every vertex in a graph that has a cycle decomposition must have even degree.

Cycle decomposition of 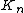and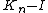

Brian Alspach and Heather Gavlas established necessary and sufficient conditions for the existence of a decomposition of a complete graph of even order minus a 1-factor into even cycles and a complete graph of odd order into odd cycles.^[1] Their proof relies on Cayley graphs, in particular, circulant graphs, and many of their decompositions come from the action of a permutation on a fixed subgraph.

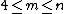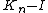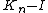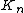They proved that for positive even integers and with ,the graph (where is a 1-factor) can be decomposed into cycles of length if and only if the number of edges in is a multiple of . Also, for positive odd integers and with 3≤m≤n, the graph can be decomposed into cycles of length if and only if the number of edges in 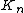is a multiple of .

References

1. ^{{cite journal|url = http://www.sciencedirect.com/science/article/pii/S0095895600919968 | doi=10.1006/jctb.2000.1996 | volume=81 | title=Cycle Decompositions of Kn and Kn−I | year=2001 | journal=Journal of Combinatorial Theory, Series B | pages=77–99 | last1 = Alspach | first1 = Brian}}

{{citation|last1=Bondy|first1=J.A.|last2=Murty|first2=U.S.R.|title=Graph Theory|publisher=Springer|year=2008|isbn=978-1-84628-969-9|chapter=2.4 Decompositions and coverings}}.

1 : Graph theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。