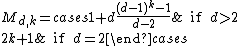“Degree diameter problem”的意思、由来-开放百科全书

词条

Degree diameter problem

释义

Formula
See also
References

In graph theory, the degree diameter problem is the problem of finding the largest possible graph G (in terms of the size of its vertex set V) of diameter k such that the largest degree of any of the vertices in G is at most d. The size of G is bounded above by the Moore bound; for 1 < k and 2 < d only the Petersen graph, the Hoffman-Singleton graph, and possibly one more graph (not yet proven to exist) of diameter k = 2 and degree d = 57 attain the Moore bound. In general, the largest degree-diameter graphs are much smaller in size than the Moore bound.

Formula

Let 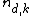be the maximum possible number of vertices for a graph with degree at most d and diameter k. Then 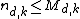, where 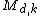is the Moore bound:

This bound is attained for very few graphs, thus the study moves to how close there exist graphs to the Moore bound.

For asymptotic behaviour note that .

Define the parameter 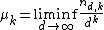. It is conjectured that 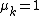for all k. It is known that 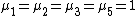and that 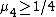. For the general case it is known that 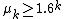. Thus, although it is conjectured that 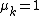, it is still an open question whether it is in fact exponential.

References

{{citation

| last1 = Bannai
| first1 = E.
| last2 = Ito
| first2 = T.
| title = On Moore graphs
| journal = J. Fac. Sci. Univ. Tokyo Ser. A
| volume = 20
| pages = 191–208
| year = 1973
| mr = 0323615 }}

{{citation

| author1-link = Alan Hoffman (mathematician)
| last1 = Hoffman
| first1 = Alan J.
| last2 = Singleton
| first2 = Robert R.
| title = Moore graphs with diameter 2 and 3
| journal = IBM Journal of Research and Development
| volume = 5
| issue = 4
| year = 1960
| pages = 497–504
| url = http://www.research.ibm.com/journal/rd/045/ibmrd0405H.pdf
| mr = 0140437
| doi=10.1147/rd.45.0497}}

{{citation

| title = There is no irregular Moore graph
| last = Singleton
| first = Robert R.
| journal = American Mathematical Monthly
| volume = 75
| issue = 1
| pages = 42–43
| year = 1968
| jstor = 2315106
| mr = 0225679
| doi = 10.2307/2315106
| publisher = Mathematical Association of America}}

{{citation

| last1 = Miller
| first1 = Mirka
| last2 = Širáň
| first2 = Jozef
| title = Moore graphs and beyond: A survey of the degree/diameter problem
| journal = Electronic Journal of Combinatorics
| volume = Dynamic survey
| pages = DS14
| year = 2005
| url = http://www.combinatorics.org/ojs/index.php/eljc/article/download/DS14/pdf}}

{{citation

| title = CombinatoricsWiki - The Degree/Diameter Problem
| url = http://combinatoricswiki.org/wiki/The_Degree/Diameter_Problem}}

1 : Computational problems in graph theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Formula

See also

References