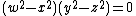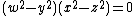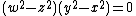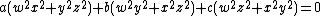“Desmic system”的意思、由来-开放百科全书

词条

Desmic system

释义

Example
References
External links

In projective geometry, a desmic system is a set of three tetrahedra in 3-dimensional projective space, such that any two are desmic, (i.e. related such that each edge of one cuts a pair of opposite edges of the other). It was introduced by {{harvs|txt|authorlink=Cyparissos Stephanos|last=Stephanos|year=1879}}. The three tetrahedra of a desmic system are contained in a pencil of quartic surfaces. The name "desmic" comes from the Greek word δεσμός, meaning band or chain, referring to the pencil of quartics.

Every line that passes through two vertices of two tetrahedra in the system also passes through a vertex of the third tetrahedron.

The 12 vertices of the desmic system and the 16 lines formed in this way are the points and lines of a Reye configuration.

Example

The three tetrahedra given by the equations

form a desmic system, contained in the pencil of quartics

for a + b + c = 0.

References

{{Citation | last1=Borwein | first1=Peter B | authorlink = Peter Borwein | title=The Desmic conjecture | doi=10.1016/0097-3165(83)90022-5 | mr=704251 | year=1983 | journal=Journal of Combinatorial Theory | series = Series A | volume=35 | issue=1 | pages=1–9}}.
{{Citation | authorlink=R. W. H. T. Hudson | last1=Hudson | first1=R. W. H. T. | title=Kummer's quartic surface | publisher=Cambridge University Press | series=Cambridge Mathematical Library | isbn=978-0-521-39790-2 | mr=1097176 | year=1990|url=https://archive.org/details/184605691}}.
{{Citation | last1=Stephanos | first1=Cyparissos | title= Sur les systèmes desmiques de trois tétraèdres | url=http://www.numdam.org/item?id=BSMA_1879_2_3_1_424_1 |jfm=11.0431.01 | year=1879 | journal=Bulletin des sciences mathématiques et astronomiques, Sér. 2 | volume=3 | issue=1 | pages= 424–456 }}.

External links

Desmic tetrahedra

1 : Projective geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。