“Diffiety”的意思、由来-开放百科全书

词条

Diffiety

释义

See also
References
External links

In mathematics a diffiety, is a geometrical object introduced by {{harvtxt|Vinogradov|1984}} playing the same role in the modern theory of partial differential equations as algebraic varieties play for algebraic equations.

In a bit more detail, a diffiety is the following: First, one defines Jet Bundles in which one can embed

submanifolds that have attached to every point kth order tangent spaces (e.g. the first order is the usual tangent

space at that point, the infinite order is the manifold itself at that point). These submanifolds of k-order Jets can then locally be parameterised by coordinates 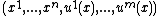together with derivatives 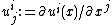of the 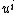up to kth order. Thus these coordinates

can naturally serve to parameterise solutions of a kth order PDE, say .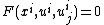

The jet-submanifold that is locally described by these coordinates itself is by construction a geometric object and thus diffeomorphism invariant (which is not the case for one of its corresponding labels 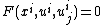which might change its form upon a change of variables).

As differentiations of the PDE lead to higher order Jet spaces that represent the same PDE, one obtains a whole

chain of Jets that represents one equation. This chain can then be studied with methods of cohomology. This

generalises the concept of an algebraic variety as (the ideal of a) solution set of an algebraic equation to the

(ideal of a) solution set of a PDE called diffiety. These diffieties are equipped with a contact structure needed for

integration. The diffieties together with maps that preserve this contact structure are the objects and Morphisms

of the Category of PDEs defined by Vinogradov. A thorough introduction to the topic is given in {{harvtxt|Vinogradov|2001}}.

Another way of generalizing ideas from algebraic geometry is differential algebraic geometry.

References

{{Citation | last1=Vinogradov | first1=A. M. | title=Local symmetries and conservation laws | doi=10.1007/BF01405491 | mr=736872 | year=1984 | journal=Acta Applicandae Mathematicae | volume=2 | issue=1 | pages=21–78}}
{{Citation | first1=Aleksandr Mikhaĭlovich | last1=Vinogradov | title=Cohomological analysis of partial differential equations and secondary calculus| year = 2001 | url = https://books.google.com/books?id=XIve9AEZgZIC| publisher= AMS Bookstore | ISBN = 978-0-8218-2922-6}}

External links

The Diffiety Institute (frozen since 2010 but contains useful, related material)
[https://sites.google.com/site/levicivitainstitute/ The Levi-Civita Institute] (successor of above site with current information on diffiety schools)
[https://gdeq.org/Welcome_to_GDEq.org! Geometry of Differential Equations]

2 : Homological algebra|Partial differential equations

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References

External links