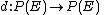- Definition
- Examples
- References
In mathematics, specifically set theory, a dimensional operator on a set E is a function from the subsets of E to the subsets of E.
Definition
If the power set of E is denoted P(E) then a dimensional operator on E is a map
that satisfies the following properties for S,T ∈ P(E):
- S ⊆ d(S);
- d(S) = d(d(S)) (d is idempotent);
- if S ⊆ T then d(S) ⊆ d(T);
- if Ω is the set of finite subsets of S then d(S) = ∪A∈Ωd(A);
- if x ∈ E and y ∈ d(S ∪ {x}) \\ d(S), then x ∈ d(S ∪ {y}).
The final property is known as the exchange axiom.[1]
Examples
- For any set E the identity map on P(E) is a dimensional operator.
- The map which takes any subset S of E to E itself is a dimensional operator on E.
References
1. ^Julio R. Bastida, Field Extensions and Galois Theory, Addison-Wesley Publishing Company, 1984, pp. 212–213.
1 : Set theory
- Waterford by-election, 1947
- Waterford by-election, 1952
- Waterford by-election, 1966
- Waterford & Central Ireland Railway
- Waterford City and County Council election, 2014
- Waterford City by-election, 1869
- Waterford City by-election, 1891
- Waterford City by-election, 1918
- Waterford City Council election, 1991
- Waterford City Council election, 1999
- Waterford City Council election, 2004
- Waterford City Council election, 2009
- Waterford City & County
- Waterford Commons
- Waterford Country School
- Waterford County by-election, 1873
- Waterford County by-election, 1877
- Waterford County Council election, 1991
- Waterford County Council election, 1999
- Waterford County Council election, 2004
- Waterford County Council election, 2009
- Waterford Crystal F.C.
- Waterford Durant High School
- Waterford (Dáil Éireann constituency)
- Waterford Film Festival