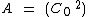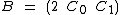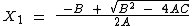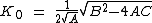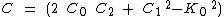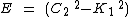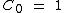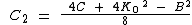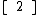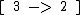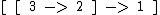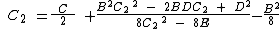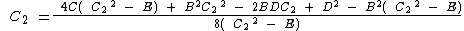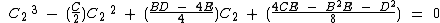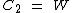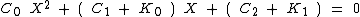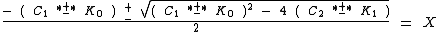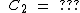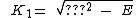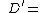- Quadratic Solution (Derived) via Reduction Mechanism
- Quartic Solution (Derived)
- Quartic Solution (Closed Form)
- References
- External links
The reduction mechanism reduces polynomials of order 2^n into two polynomials of order 2^(n-1). The purpose is to reduce polynomials into an order which can be solved with a closed form equation. The simplest example of this is reducing an order 2 polynomial into two order 1 polynomials; a quadratic into two linear equations.
Quadratic Solution (Derived) via Reduction Mechanism
Begin with 
 &
& 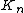 ∈ ℂ
∈ ℂ
In general this equation can be solved using 2 methods.
(1) : Take the positive and negative of one side.



(a)
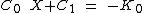


(b)
Making X the subject yields
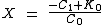


(a')



(b')
(2) : Square both sides to remove the modulus.



(c)
Equating equation (c) to the general quadratic 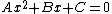 gives
gives
A, B and C are all constants, therefore  and
and 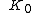 can be expressed in terms of A, B and C
can be expressed in terms of A, B and C
Substituting these new values for  and
and 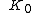 into equations (a') and (b') yields the 2 roots of a quadratic.
into equations (a') and (b') yields the 2 roots of a quadratic.
Combining these two equations together gives the more general solution to the quadratic
This can also be written in the modulus form.
,
Quartic Solution (Derived)
Begin with 
 &
& 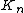 ∈ ℂ
∈ ℂ
In general this equation can be solved using 2 methods.
(1) : Take the positive and negative of one side.
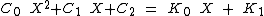


(a)



(b)
(2) : Square both sides to remove the modulus.



(c)
Equating equation (c) to the general quartic 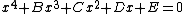 gives
gives
(note) This is still a general equation since dividing by A does not change the roots
(note) -1 can be used, the effect will be explained at the end.
Notice that  &
&  have not yet been solved. This can be resolved by forming a cubic equation in
have not yet been solved. This can be resolved by forming a cubic equation in 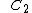
[NEEDS LOOKING UP] - Exact solution for general cubic equation
Let the solutions to this equation be 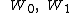 &
&  each of which can be determined by using the closed form solution to the general cubic. Any of these values are usable, so we shall just call our solution W.
each of which can be determined by using the closed form solution to the general cubic. Any of these values are usable, so we shall just call our solution W.
Now that we have a usable value for 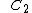 we can find respective values for
we can find respective values for 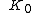 &
&  , so we have:
, so we have:
Substituting these values into method 1 gives a general solution for the quartic.
[4]
[5]
[4]
[5]
Root 1 = + *+*
Root 2 = + *-*
Root 3 = - *+*
Root 4 = - *-*
A show as to why  can be 1 or -1 and why all 3 values of W work:
can be 1 or -1 and why all 3 values of W work:
Notice how the four roots of the general quartic are split into pairs, via the two equations in method 1. There are six different ways of laying out the roots as shown below.




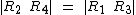

The second set of values is the reverse of the first set. Which way round the roots come out is determined by whether 1 or -1 is the value of 
The three different arrangements within the 2 sets are determined by the value of W chosen.
Below is the general solution when  = 1 and W is the first root of a cubic. [The first root being the real root determined by the formula when there is only 1 real root]
= 1 and W is the first root of a cubic. [The first root being the real root determined by the formula when there is only 1 real root]
Quartic Solution (Closed Form)
To solve:
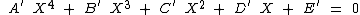
First divide through by A to get:

Then put values for each of the constants into the formula below.
References
External links
- example.com
- PIE root
- Piero Pasinati
- Piero Pelu
- Piero Pelù
- Piero Pierantoni Cámpora
- Piero Pisenti
- Piero Pollaiuolo
- Piero Scaruffi
- Piero sicoli
- Piero Strozzi
- Piero the Fatuous
- Piero Torrigiano
- Piero Toscani
- Pie Rouge des Plaines
- Pie rouge des plaines
- Pie Rouge Des Plaines
- Pierozhki
- Pier Paolo Bianchi
- Pierpaolo Ferrazzi
- Pier Paolo Pandolfi
- Pier Paolo Polcari
- Pier Paolo Vergerio the Elder
- Pier Paolo Vergerio the younger
- Pier Paulo Pasolini
- Pier Paulo Vergerio