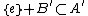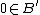“Dyson's transform”的意思、由来-开放百科全书

Dyson's transform is a fundamental technique in additive number theory.^[1] It was developed by Freeman Dyson as part of his proof of Mann's theorem,^[2]{{Rp|17}} is used to prove such fundamental results of Additive Number Theory as the Cauchy-Davenport theorem,^[1] and was used by Olivier Ramaré in his work on the Goldbach conjecture that proved that every even integer is the sum of at most 6 primes.^[3]{{Rp|700–701}} The term Dyson's transform for this technique is used by Ramaré.^[3]{{Rp|700–701}} Halberstam and Roth call it the τ-transformation.^[2]{{Rp|58}}

This formulation of the transform is from Ramaré.^[3]{{Rp|700–701}} Let A be a sequence of natural numbers, and x be any real number. Write A(x) for the number of elements of A which lie in [1, x]. Suppose

and

are two sequences of natural numbers. We write A + B for the sumset, that is, the set of all elements a + b where a is in A and b is in B; and similarly A − B for the set of differences a − b. For any element e in A, Dyson's transform consists in forming the sequences

and

. The transformed sequences have the properties:

References

1. ^¹Additive Number Theory: Inverse Problems and the Geometry of Sumsets By Melvyn Bernard Nathanson, Springer, Aug 22, 1996, {{ISBN|0-387-94655-1}}, https://books.google.com/books?id=PqlQjNhjkKUC&dq=%22e-transform%22&source=gbs_navlinks_s, p. 42
2. ^¹{{cite book | last1 = Halberstam | first1 = H. |authorlink1 = Heini Halberstam | last2 = Roth | first2 = K. F. | authorlink2 =Klaus Roth | title = Sequences | publisher = Springer-Verlag | location = Berlin | year = 1983 | edition = revised | isbn = 978-0-387-90801-4 }}
3. ^¹²{{cite journal | author=O. Ramaré | authorlink=Olivier Ramaré | title=On šnirel'man's constant | journal=Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV | volume=22 | year=1995 | issue=4 | pages=645–706 | url = http://www.numdam.org/item?id=ASNSP_1995_4_22_4_645_0 | accessdate = 2009-03-13}}