“Essential dimension”的意思、由来-开放百科全书

词条

Essential dimension

释义

Formal definition
Examples
Known results
References

In mathematics, essential dimension is an invariant defined for certain algebraic structures such as algebraic groups and quadratic forms. It was introduced by J. Buhler and Z. Reichstein ^[1]

and in its most generality defined by A. Merkurjev.

^[2]

Basically, essential dimension measures the complexity of algebraic structures via their fields of definition. For example, a quadratic form q : V → K over a field K, where V is a K-vector space, is said to be defined over a subfield L of K if there exists a K-basis e₁,...,e_n of V such that q can be expressed in the form with all coefficients a_ij belonging to L. If K has characteristic different from 2, every quadratic form is diagonalizable. Therefore, q has a field of definition generated by n elements. Technically, one always works over a (fixed) base field k and the fields K and L in consideration are supposed to contain k. The essential dimension of q is then defined as the least transcendence degree over k of a subfield L of K over which q is defined.

Formal definition

Fix an arbitrary field k and let Fields/k denote the category of finitely generated field extensions of k with inclusions as morphisms. Consider a (covariant) functor F : Fields/k → Set.

For a field extension K/k and an element a of F(K/k) a field of definition of a is an intermediate field K/L/k such that a is contained in the image of the map F(L/k) → F(K/k) induced by the inclusion of L in K.

The essential dimension of a, denoted by ed(a), is the least transcendence degree (over k) of a field of definition for a. The essential dimension of the functor F, denoted by ed(F), is the supremum of ed(a) taken over all elements a of F(K/k) and objects K/k of Fields/k.

Examples

Essential dimension of quadratic forms: For a natural number n consider the functor Q_n : Fields/k → Set taking a field extension K/k to the set of isomorphism classes of non-degenerate n-dimensional quadratic forms over K and taking a morphism L/k → K/k (given by the inclusion of L in K) to the map sending the isomorphism class of a quadratic form q : V → L to the isomorphism class of the quadratic form .
Essential dimension of algebraic groups: For an algebraic group G over k denote by H¹(-,G) : Fields/k → Set the functor taking a field extension K/k to the set of isomorphism classes of G-torsors over K (in the fppf-topology). The essential dimension of this functor is called the essential dimension of the algebraic group G, denoted by ed(G).
Essential dimension of a fibered category: Let be a category fibered over the category of affine k-schemes, given by a functor For example, may be the moduli stack of genus g curves or the classifying stack of an algebraic group. Assume that for each 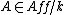the isomorphism classes of objects in the fiber p⁻¹(A) form a set. Then we get a functor F_p : Fields/k → Set taking a field extension K/k to the set of isomorphism classes in the fiber . The essential dimension of the fibered category is defined as the essential dimension of the corresponding functor F_p. In case of the classifying stack 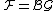of an algebraic group G the value coincides with the previously defined essential dimension of G.

Known results

The essential dimension of a linear algebraic group G is always finite and bounded by the minimal dimension of a generically free representation minus the dimension of G.
The essential dimension of a finite algebraic p-group over k equals the minimal dimension of a faithful representation, provided that the base field k contains a primitive p-th root of unity.
The essential dimension of the symmetric group S_n (viewed as algebraic group over k) is known for n≤5 (for every base field k), for n=6 (for k of characteristic not 2) and for n=7 (in characteristic 0).
Let T be an algebraic torus admitting a Galois splitting field L/k of degree a power of a prime p. Then the essential dimension of T equals the least rank of the kernel of a homomorphism of Gal(L/k)-lattices P → X(T) with cokernel finite and of order prime to p, where P is a permutation lattice.

References

1. ^{{cite journal|title=On the essential dimension of a finite group|journal=Compositio Mathematica|year=1997|first=J.|last=Buhler|author2=Reichstein, Z. |volume=106|issue=2|pages=159–179|id= |url=|format=|doi=10.1023/A:1000144403695 }}
2. ^{{cite journal|title=Essential Dimension: a Functorial Point of View (after A. Merkurjev)|journal=Documenta Mathematica|year=2003|first=G.|last=Berhuy|author2=Favi, G. |volume=8|issue=|pages=279–330 (electronic)|id= |format=}}

1 : Algebraic structures

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。