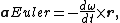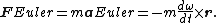“Euler force”的意思、由来-开放百科全书

In classical mechanics, the Euler force is the fictitious tangential force that is felt in reaction to any angular acceleration. That reactive acceleration is the Euler acceleration (named for Leonhard Euler), also known as azimuthal acceleration^[1] or transverse acceleration.^[2] It is an acceleration that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes. This article is restricted to a reference frame that rotates about a fixed axis.

The Euler force is related to the Euler acceleration by F = ma, where a is the Euler acceleration and m is the mass of the body.^[3]^[4]

Intuitive example

The Euler force will be felt by a person riding a merry-go-round. As the ride starts, the Euler force will be the apparent force pushing the person to the back of the horse, and as the ride comes to a stop, it will be the apparent force pushing the person towards the front of the horse. A person on a horse close to the perimeter of the merry-go-round will perceive a greater apparent force than a person on a horse closer to the axis of rotation.

The Euler force is perpendicular to the centrifugal force and is in the plane of rotation.

Mathematical description

where ω is the angular velocity of rotation of the reference frame and r is the vector position of the point where the acceleration is measured relative to the axis of the rotation. The Euler force on an object of mass m is then

See also

Notes and references

1. ^{{cite book |author=David Morin |url=https://books.google.com/books?id=Ni6CD7K2X4MC&pg=PA469&dq=acceleration+azimuthal+inauthor:Morin&lr=&as_brr=0 |title=Introduction to classical mechanics: with problems and solutions |page= 469 |isbn= 0-521-87622-2 |year=2008 |publisher=Cambridge University Press}}
2. ^{{cite book |author=Grant R. Fowles and George L. Cassiday|title=Analytical Mechanics, 6th ed.|page=178|year=1999|publisher=Harcourt College Publishers}}
3. ^{{cite book |title=An introduction to the mathematics and methods of astrodynamics |page=102 |author= Richard H Battin |url=https://books.google.com/books?id=OjH7aVhiGdcC&pg=PA102&vq=Euler&dq=%22Euler+acceleration%22&lr=&as_brr=0&source=gbs_search_s&sig=ACfU3U0__alj4q5o16OHM8vGvArm0rqMdg|isbn=1-56347-342-9 |year=1999 |publisher=American Institute of Aeronautics and Astronautics |location=Reston, VA }}
4. ^{{cite book |title=Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems |author=Jerrold E. Marsden, Tudor S. Ratiu |isbn=0-387-98643-X |year=1999 |publisher=Springer |page=251 |url=https://books.google.com/books?id=I2gH9ZIs-3AC&pg=PP1&dq=isbn:038798643X&sig=tDWUiGpvGVpbRCCQcGK0Bx5Yk3g#PPA251,M1}}