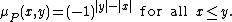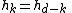“Eulerian poset”的意思、由来-开放百科全书

词条

Eulerian poset

释义

Examples
Properties
Notes
References
See also

In combinatorial mathematics, an Eulerian poset is a graded poset in which every nontrivial interval has the same number of elements of even rank as of odd rank. An Eulerian poset which is a lattice is an Eulerian lattice. These objects are named after Leonhard Euler. Eulerian lattices generalize face lattices of convex polytopes and much recent research has been devoted to extending known results from polyhedral combinatorics, such as various restrictions on f-vectors of convex simplicial polytopes, to this more general setting.

Examples

The face lattice of a convex polytope, consisting of its faces, together with the smallest element, the empty face, and the largest element, the polytope itself, is an Eulerian lattice. The odd–even condition follows from Euler's formula.
Any simplicial generalized homology sphere is an Eulerian lattice.
Let L be a regular cell complex such that |L| is a manifold with the same Euler characteristic as the sphere of the same dimension (this condition is vacuous if the dimension is odd). Then the poset of cells of L, ordered by the inclusion of their closures, is Eulerian.
Let W be a Coxeter group with Bruhat order. Then (W,≤) is an Eulerian poset.

Properties

The defining condition of an Eulerian poset P can be equivalently stated in terms of its Möbius function:

The dual of an Eulerian poset, obtained by reversing the partial order, is Eulerian.
Richard Stanley defined the toric h-vector of a ranked poset, which generalizes the h-vector of a simplicial polytope.^[1] He proved that the Dehn–Sommerville equations

hold for an arbitrary Eulerian poset of rank d + 1.^[2] However, for an Eulerian poset arising from a regular cell complex or a convex polytope, the toric h-vector neither determines, nor is neither determined by the numbers of the cells or faces of different dimension and the toric h-vector does not have a direct combinatorial interpretation.

Notes

1. ^Enumerative combinatorics, 3.14, p. 138; formerly called the generalized h-vector.
2. ^Enumerative combinatorics, Theorem 3.14.9

References

Richard P. Stanley, Enumerative Combinatorics, Volume 1. Cambridge University Press, 1997 {{ISBN|0-521-55309-1}}

Examples

Properties

Notes

References

See also