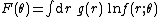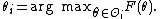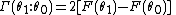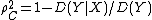- Definition in terms of information gain Information gain by better modelling Information gain by a conditional model
- Special cases and generalized usage Linear regression Correlation coefficient as measure of explained variance In principal component analysis
- Criticism
- See also
- References
- External links
In statistics, explained variation measures the proportion to which a mathematical model accounts for the variation (dispersion) of a given data set. Often, variation is quantified as variance; then, the more specific term explained variance can be used.
The complementary part of the total variation is called unexplained or residual variation.
Definition in terms of information gain
Information gain by better modelling
Following Kent (1983),[1] we use the Fraser information (Fraser 1965)[2]
where  is the probability density of a random variable
is the probability density of a random variable 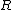 , and
, and 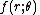 with
with 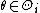 (
(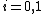 ) are two families of parametric models. Model family 0 is the simpler one, with a restricted parameter space
) are two families of parametric models. Model family 0 is the simpler one, with a restricted parameter space 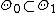 .
.
Parameters are determined by maximum likelihood estimation,
The information gain of model 1 over model 0 is written as
where a factor of 2 is included for convenience. Γ is always nonnegative; it measures the extent to which the best model of family 1 is better than the best model of family 0 in explaining g(r).
Information gain by a conditional model
Assume a two-dimensional random variable 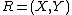 where X shall be considered as an explanatory variable, and Y as a dependent variable. Models of family 1 "explain" Y in terms of X,
where X shall be considered as an explanatory variable, and Y as a dependent variable. Models of family 1 "explain" Y in terms of X,
,
whereas in family 0, X and Y are assumed to be independent. We define the randomness of Y by 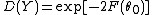 , and the randomness of Y, given X, by
, and the randomness of Y, given X, by 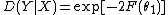 . Then,
. Then,
can be interpreted as proportion of the data dispersion which is "explained" by X.
Special cases and generalized usage
Linear regression
{{main|Fraction of variance unexplained}}The fraction of variance unexplained is an established concept in the context of linear regression. The usual definition of the coefficient of determination is based on the fundamental concept of explained variance.
Correlation coefficient as measure of explained variance
Let X be a random vector, and Y a random variable that is modeled by a normal distribution with centre 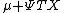 . In this case, the above-derived proportion of explained variation
. In this case, the above-derived proportion of explained variation 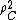 equals the squared correlation coefficient
equals the squared correlation coefficient  .
.
Note the strong model assumptions: the centre of the Y distribution must be a linear function of X, and for any given x, the Y distribution must be normal. In other situations, it is generally not justified to interpret  as proportion of explained variance.
as proportion of explained variance.
In principal component analysis
Explained variance is routinely used in principal component analysis. The relation to the Fraser–Kent information gain remains to be clarified.
Criticism
As the fraction of "explained variance" equals the squared correlation coefficient  , it shares all the disadvantages of the latter: it reflects not only the quality of the regression, but also the distribution of the independent (conditioning) variables.
, it shares all the disadvantages of the latter: it reflects not only the quality of the regression, but also the distribution of the independent (conditioning) variables.
In the words of one critic: "Thus  gives the 'percentage of variance explained' by the regression, an expression that, for most social scientists, is of doubtful meaning but great rhetorical value. If this number is large, the regression gives a good fit, and there is little point in searching for additional variables. Other regression equations on different data sets are said to be less satisfactory or less powerful if their
gives the 'percentage of variance explained' by the regression, an expression that, for most social scientists, is of doubtful meaning but great rhetorical value. If this number is large, the regression gives a good fit, and there is little point in searching for additional variables. Other regression equations on different data sets are said to be less satisfactory or less powerful if their  is lower. Nothing about
is lower. Nothing about  supports these claims".[3]{{rp|58}} And, after constructing an example where
supports these claims".[3]{{rp|58}} And, after constructing an example where  is enhanced just by jointly considering data from two different populations: "'Explained variance' explains nothing."[3]{{Page needed|date=February 2013}}[4]{{rp|183}}
is enhanced just by jointly considering data from two different populations: "'Explained variance' explains nothing."[3]{{Page needed|date=February 2013}}[4]{{rp|183}}
See also
- Analysis of variance
- Variance reduction
- Variance-based sensitivity analysis
References
2. ^{{cite journal |first=D. A. S. |last=Fraser |year=1965 |title=On Information in Statistics |journal=Ann. Math. Statist. |volume=36 |issue=3 |pages=890–896 |doi=10.1214/aoms/1177700061 }}
3. ^1 {{cite book |first=C. H. |last=Achen |year=1982 |title=Interpreting and Using Regression |location=Beverly Hills |publisher=Sage |isbn=0-8039-1915-8 }}
4. ^{{cite journal |first=C. H. |last=Achen |year=1990 |title='What Does "Explained Variance" Explain?: Reply |journal=Political Analysis |volume=2 |issue=1 |pages=173–184 |doi=10.1093/pan/2.1.173 }}
External links
- Variance, explained and unexplained
- [https://web.archive.org/web/20080413144223/http://darwin.cwru.edu/~witte/statistics/explained_variance.htm Explained and Unexplained Variance on a graph]
- The Secret of The Sirens
- The secret of the sirens
- The Secret of the Sirens
- The Secret of the Storm Country
- The Secret of the Submarine
- The Secret of Three Points
- The Secret of Wilhelm Storitz
- The Secret Order Of The Gumm Street Girls
- The Secret Order of the Gumm Street Girls
- The Secret Partner
- The Secret Peacemaker
- The Secret Place (film)
- The Secret Policeman's Ball (2008)
- The Secret Policeman's Ball 2008
- The Secret Policeman's Ball mediagraphy
- The Secret Policeman's Balls (DVD box set)
- The Secret Policeman's Balls releases
- The Secret Policeman's Third Ball
- The Secret Public Years 1981-1989
- The Secret Radio Project
- The Secret Rapture
- The Secret Rapture (film)
- The Secret Rapture (play)
- The Secret Relationship Between Blacks and Jews
- The Secret relationship between Blacks and Jews