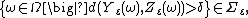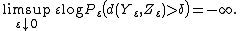“Exponentially equivalent measures”的意思、由来-开放百科全书

词条

Exponentially equivalent measures

释义

Definition
Properties
References

In mathematics, exponential equivalence of measures is how two sequences or families of probability measures are “the same” from the point of view of large deviations theory.

Definition

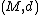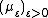Let be a metric space and consider two one-parameter families of probability measures on , say and 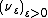. These two families are said to be exponentially equivalent if there exist

a one-parameter family of probability spaces ,
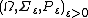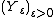two families of -valued random variables and ,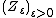

such that

for each , the 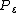-law (i.e. the push-forward measure) of 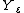is 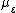, and the 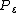-law of 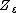is ,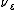
for each 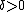, “ 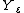and 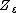are further than apart” is a 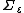-measurable event, i.e.

for each ,

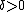The two families of random variables 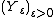and 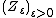are also said to be exponentially equivalent.

Properties

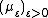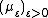The main use of exponential equivalence is that as far as large deviations principles are concerned, exponentially equivalent families of measures are indistinguishable. More precisely, if a large deviations principle holds for with good rate function , and and 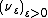are exponentially equivalent, then the same large deviations principle holds for 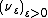with the same good rate function .

References

{{cite book

}} (See section 4.2.2)

3 : Asymptotic analysis|Probability theory|Equivalence (mathematics)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。