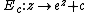- Family
- Forms
- References
In the theory of dynamical systems, the exponential map can be used as the evolution function of the discrete nonlinear dynamical system.[1]
Family
The family of exponential functions is called the exponential family.
Forms
There are many forms of these maps,[2] many of which are equivalent under a coordinate transformation. For example two of the most common ones are:
The second one can be mapped to the first using the fact that 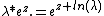 , so
, so 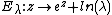 is the same under the transformation
is the same under the transformation 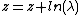 . The only difference is that, due to multi-valued properties of exponentiation, there may be a few select cases that can only be found in one version. Similar arguments can be made for many other formulas.
. The only difference is that, due to multi-valued properties of exponentiation, there may be a few select cases that can only be found in one version. Similar arguments can be made for many other formulas.
References
1. ^Dynamics of exponential maps by Lasse Rempe
2. ^Lasse Rempe, Dierk Schleicher : Bifurcation Loci of Exponential Maps and Quadratic Polynomials: Local Connectivity, Triviality of Fibers, and Density of Hyperbolicity
{{Commons category|Exponential maps}}{{Wikibooks|Fractals/exponential}}{{Chaos theory}}{{geometry-stub}}2. ^Lasse Rempe, Dierk Schleicher : Bifurcation Loci of Exponential Maps and Quadratic Polynomials: Local Connectivity, Triviality of Fibers, and Density of Hyperbolicity
1 : Chaotic maps
- International Business College Indianapolis, IN
- International Business College Indianapolis, Indiana
- International business corporation
- International Business Council of Florida
- International business development
- International Business District station
- International Business Entry Modes
- International Business Machines Corporation v. Papermaster
- International Business Machines Corp. v. Papermaster
- International Business School (disambiguation)
- International Business School of Scandinavia
- International Business School of Vilnius University
- International business study
- International Cable Protection Committee
- International calendar
- International call sign
- International call signs
- International Campus for Advanced Studies
- International Cancer Genome Consortium
- International Cancer Research
- International Canine Federation
- International canoe
- International capital market association
- International Capital Markets Association
- INTERNATIONAL CAPSLOCK DAY