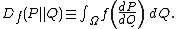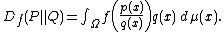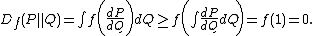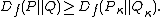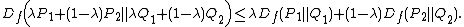- Definition
- Instances of f-divergences
- Properties
- References
In probability theory, an ƒ-divergence is a function Df (P || Q) that measures the difference between two probability distributions P and Q. It helps the intuition to think of the divergence as an average, weighted by the function f, of the odds ratio given by P and Q.
These divergences were introduced and studied independently by {{harvtxt|Csiszár|1963}}, {{harvtxt|Morimoto|1963}} and {{harvtxt|Ali|Silvey|1966}} and are sometimes known as Csiszár ƒ-divergences, Csiszár-Morimoto divergences or Ali-Silvey distances.
Definition
Let P and Q be two probability distributions over a space Ω such that P is absolutely continuous with respect to Q. Then, for a convex function f such that f(1) = 0, the f-divergence of P from Q is defined as
If P and Q are both absolutely continuous with respect to a reference distribution μ on Ω then their probability densities p and q satisfy dP = p dμ and dQ = q dμ. In this case the f-divergence can be written as
The f-divergences can be expressed using Taylor series and rewritten using a weighted sum of chi-type distances ({{harvtxt|Nielsen|Nock|2013}}).
Instances of f-divergences
Many common divergences, such as KL-divergence, Hellinger distance, and total variation distance, are special cases of f-divergence, coinciding with a particular choice of f. The following table lists many of the common divergences between probability distributions and the f function to which they correspond (cf. {{harvtxt|Liese|Vajda|2006}}).
| Divergence | Corresponding f(t) |
|---|---|
| KL-divergence | 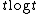 |
| reverse KL-divergence | 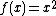 |
| Hellinger distance | 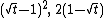 |
| Total variation distance | 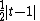 |
Pearson  -divergence -divergence | 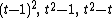 |
Neumann  -divergence (reverse Pearson's) -divergence (reverse Pearson's) | 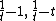 |
| α-divergence | 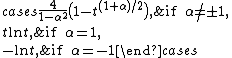 |
| α-divergence (other designation) | 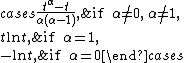 |
It should be noted that the function  is defined up to the summand
is defined up to the summand 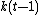 , where
, where  is any constant.
is any constant.
Properties
{{unordered list|1= Non-negativity: the ƒ-divergence is always positive; it's zero if and only if the measures P and Q coincide. This follows immediately from Jensen’s inequality:
|2= Monotonicity: if κ is an arbitrary transition probability that transforms measures P and Q into Pκ and Qκ correspondingly, then
The equality here holds if and only if the transition is induced from a sufficient statistic with respect to {P, Q}.
|3= Joint Convexity: for any {{nowrap|0 ≤ λ ≤ 1}}
This follows from the convexity of the mapping 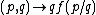 on
on 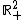 .
.
}}
References
{{refbegin}}- {{cite journal
| first = I.
| last = Csiszár
| year = 1963
| title = Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis der Ergodizitat von Markoffschen Ketten
| journal = Magyar. Tud. Akad. Mat. Kutato Int. Kozl
| volume = 8
| pages = 85–108
| ref = CITEREFCsisz.C3.A1r1963
- {{cite journal
| doi = 10.1143/JPSJ.18.328
| first = T.
| last = Morimoto
| year = 1963
| title = Markov processes and the H-theorem
| journal = J. Phys. Soc. Jpn.
| volume = 18
| issue = 3
| pages = 328–331
| ref = CITEREFMorimoto1963
| bibcode = 1963JPSJ...18..328M
- {{cite journal
| first1 = S. M. | last1 = Ali
| first2 = S. D. | last2 = Silvey
| year = 1966
| title = A general class of coefficients of divergence of one distribution from another
| journal = Journal of the Royal Statistical Society, Series B
| volume = 28
| issue = 1
| pages = 131–142
| jstor = 2984279 | mr = 0196777
| ref = CITEREFAliSilvey1966
- {{cite journal
| first = I.
| last = Csiszár
| year = 1967
| title = Information-type measures of difference of probability distributions and indirect observation
| journal = Studia Scientiarum Mathematicarum Hungarica
| volume = 2
| pages = 229–318
| ref = CITEREFCsisz.C3.A1r1967
- {{cite journal
| first1 = I. | last1 = Csiszár | authorlink1 = Imre Csiszár
| first2 = P. | last2 = Shields
| year = 2004
| title = Information Theory and Statistics: A Tutorial
| journal = Foundations and Trends in Communications and Information Theory
| volume = 1
| issue = 4
| pages = 417–528
| doi = 10.1561/0100000004
| url = http://www.renyi.hu/~csiszar/Publications/Information_Theory_and_Statistics:_A_Tutorial.pdf
| accessdate = 2009-04-08
- {{cite journal
| first1 = F. | last1 = Liese
| first2 = I. | last2 = Vajda
| year = 2006
| title = On divergences and informations in statistics and information theory
| journal = IEEE Transactions on Information Theory
| volume = 52
| issue = 10
| pages = 4394–4412
| doi = 10.1109/TIT.2006.881731
| ref = CITEREFLieseVajda2006
- {{cite journal
| first1 = F. | last1 = Nielsen
| first2 = R. | last2 = Nock
| year = 2013
| title = On the Chi square and higher-order Chi distances for approximating f-divergences
| arxiv = 1309.3029
| ref = CITEREFNielsenNock2013
| doi=10.1109/LSP.2013.2288355
| volume=21
| journal=IEEE Signal Processing Letters
| pages=10–13
| bibcode=2014ISPL...21...10N}}
- {{cite arXiv
| first1 = J-F. | last1 = Coeurjolly
| first2 = R. | last2 = Drouilhet
| year = 2006
| title = Normalized information-based divergences
| eprint = math/0604246
| ref = arXiv:math/0604246{{refend}}
- Kilchrist Castle
- Kilchrist, County Clare
- Kilciler, Goynuk
- Kilciler, Göynük
- Kil class sloop
- Kil-class sloop
- Kilcleagh, (civil parish)
- Kilcleagh (civil parish)
- Kilclief
- Kilclooney More
- Kilcloony
- Kilcock Novice Chase
- Kilcoe railway station
- Kilcolman Abbey
- Kilcommon and Hollyford and Rearcross
- Kilconry
- Kilcoole halt
- Kilcooly
- Kilcooly (civil parish)
- Kilcooly (disambiguation)
- Kilcooly(disambiguation)
- Kilcormac-Killoughey
- Kilcormac-Killoughey GAA
- Kilcormac/Killoughey GAA
- Kilcorney, County Clare