“Feedback with Carry Shift Registers”的意思、由来-开放百科全书

In sequence design, a Feedback with Carry Shift Register (or FCSR) is the arithmetic or with carry analog of a Linear feedback shift register (LFSR). If

is an integer, then an N-ary FCSR of length

is a finite state device with a state

consisting of a vector of elements

and an integer

.^[1]^[2]^[3]^[4] The state change operation is determined by a set of coefficients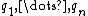

and is defined as follows: compute

. Express s as

with

. Then the new state is

. By iterating the state change an FCSR generates an infinite, eventually periodic sequence of numbers in

FCSRs have been used in the design of stream ciphers (such as the F-FCSR generator), in the cryptanalysis of the summation combiner stream cipher (the reason Goresky and Klapper invented them^[1]), and in generating pseudorandom numbers for quasi-Monte Carlo (under the name Multiply With Carry (MWC) generator - invented by Couture and L'Ecuyer,^[2]) generalizing work of Marsaglia and Zaman.^[4]

FCSRs are analyzed using number theory. Associated with the FCSR is a connection integer

. Associated with the output sequence is the N-adic number

The fundamental theorem of FCSRs says that there is an integer

so that

, a rational number. The output sequence is strictly periodic if and only if

is between

and

. It is possible to express u as a simple quadratic polynomial involving the initial state and the q_i.^[1]

There is also an exponential representation of FCSRs: if

is the inverse of

, and the output sequence is strictly periodic, then

, where

is an integer. It follows that the period is at most the order of N in the multiplicative group of units modulo q. This is maximized when q is prime and N is a primitive element modulo q. In this case, the period is

. In this case the output sequence is called an l-sequence (for "long sequence").^[1]

l-sequences have many excellent statistical properties{{r|FCSR1|efficient MWC}} that make them candidates for use in applications,^[5] including near uniform distribution of sub-blocks, ideal arithmetic autocorrelations, and the arithmetic shift and add property. They are the with-carry analog of m-sequences or maximum length sequences.

There are efficient algorithms for FCSR synthesis. This is the problem: given a prefix of a sequence, construct a minimal length FCSR that outputs the sequence. This can be solved with a variant of Mahler^[6] and De Weger's^[7] lattice based analysis of N-adic numbers when

;^[1] by a variant of the Euclidean algorithm when N is prime; and in general by Xu's adaptation of the Berlekamp-Massey algorithm.^[8] If L is the size of the smallest FCSR that outputs the sequence (called the N-adic complexity of the sequence), then all these algorithms require a prefix of length about

to be successful and have quadratic time complexity. It follows that, as with LFSRs and linear complexity, any stream cipher whose N-adic complexity is low should not be used for cryptography.

FCSRs and LFSRs are special cases of a very general algebraic construction of sequence generators called Algebraic Feedback Shift Registers (AFSRs) in which the integers are replaced by an arbitrary ring R and N is replaced by an arbitrary non-unit in R.^[9] A general reference on the subject of LFSRs, FCSRs, and AFSRs is the book.^[10]

References

1. ^¹²³⁴{{cite journal |first1=Andrew |last1=Klapper |first2=Mark |last2=Goresky |title=Feedback Shift Registers, 2-Adic Span, and Combiners With Memory |journal=Journal of Cryptology |volume=10 |issue=2 |pages=111–147 |date=March 1997 |url=http://cs.engr.uky.edu/~klapper/pdf/fcsr.pdf |citeseerx=10.1.1.37.5637 |doi=10.1007/s001459900024}}
2. ^¹{{cite journal |first1=Raymond |last1=Couture |first2=Pierre |last2=L’Ecuyer |title=On the lattice structure of certain linear congruential sequences related to AWC/SWB generators |journal=Mathematics of Computation |volume=62 |issue=206 |pages=799–808 |date=April 1994 |doi=10.2307/2153540 |doi-access=free |url=http://www.ams.org/journals/mcom/1994-62-206/S0025-5718-1994-1220826-X/S0025-5718-1994-1220826-X.pdf}}
3. ^{{cite journal |first1=Mark |last1=Goresky |first2=Andrew |last2=Klapper |title=Efficient Multiply-with-Carry Random Number Generators with Maximal Period |journal=ACM Transactions on Modeling and Computer Simulation |volume=13 |issue=4 |pages=310–321 |date=October 2003 |url=https://www.math.ias.edu/~goresky/pdf/p1-goresky.pdf |citeseerx=10.1.1.22.9007 |doi=10.1145/945511.945514}}
4. ^{{cite journal |first1=George |last1=Marsaglia |authorlink1=George Marsaglia |first2=Arif |last2=Zaman |authorlink2=Arif Zaman |title=A new class of random number generators |journal=Annals of Applied Probability |volume=1 |issue=3 |pages=462–480 |date=August 1991 |doi=10.1214/aoap/1177005878 |url=https://projecteuclid.org/download/pdf_1/euclid.aoap/1177005878 |format=pdf}}
5. ^{{cite book |first=Bruce |last=Schneier |authorlink=Bruce Schneier |title=Applied Cryptography |publisher=John Wiley & Sons |location=New York |year=1996}}
6. ^{{cite journal |first=Kurt |last=Mahler |authorlink=Kurt Mahler |title=On a geometrical representation of p-adic numbers |journal=Annals of Mathematics |series=2 |volume=41 |issue=1 |pages=8–56 |date=January 1940 |doi=10.2307/1968818 |mr=1772 |url=https://carma.newcastle.edu.au/mahler/docs/064.pdf#}}
7. ^{{cite journal |first=B. M. M. |last=de Weger |title=Approximation lattices of p–adic numbers |journal=Journal of Number Theory |volume=24 |issue=1 |pages=70–88 |date=September 1986 |doi=10.1016/0022-314X(86)90059-4 |url=http://deweger.xs4all.nl/papers/[1]dW-ApprLatt-JNumTh[1986].pdf}}
8. ^{{cite journal |first1=Andrew |last1=Klapper |first2=Jinzhong |last2=Xu |title=Register Synthesis for Algebraic Feedback Shift Registers Based on Non-Primes |journal=Designs, Codes, and Cryptography |volume=31 |issue=3 |pages=227–250 |date=March 2004 |url=http://cs.engr.uky.edu/~klapper/pdf/nfcsr.pdf}}
9. ^{{cite journal |first1=Andrew |last1=Klapper |first2=Jinzhong |last2=Xu |title=Algebraic Feedback Shift Registers |journal=Theoretical Computer Science |volume=226 |issue=1–2 |pages=61–93 |date=17 September 1999 |doi=10.1016/S0304-3975(99)00066-3 |doi-access=free |citeseerx=10.1.1.36.8645 |url=https://www.cs.uky.edu/~klapper/pdf/afsr.pdf}}
10. ^¹{{cite book |first1=Mark |last1=Goresky |first2=Andrew |last2=Klapper |title=Algebraic Shift Register Sequences |publisher=Cambridge University Press |year=2012 |isbn=978-1-107-01499-2}} Table of contents.