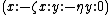- Rational curves
- References
In mathematics, a Fermat quintic threefold is a special quintic threefold, in other words a degree 5, dimension 3 hypersurface in 4-dimensional complex projective space, given by the equation
.
This threefold, so named after Pierre de Fermat, is a Calabi–Yau manifold.
The Hodge diamond of a non-singular quintic 3-fold is
{{Hodge diamond|1
|0|0
|0|1|0
|1|101|101|1
|0|1|0
|0|0
|1
}}
Rational curves
{{harvs|txt|last=Clemens|first=Herbert|authorlink=Herbert Clemens |year=1984}} conjectured that the number of rational curves of a given degree on a generic quintic threefold is finite. The Fermat quintic threefold is not generic in this sense, and {{harvs|txt| last1=Albano | first1=Alberto | last2=Katz | first2=Sheldon | authorlink2= Sheldon Katz |year=1991}} showed that its lines are contained in 50 1-dimensional families of the formfor  and
and  . There are 375 lines in more than one family, of the form
. There are 375 lines in more than one family, of the form
for fifth roots of unity  and
and  .
.
References
- {{Citation | last1=Albano | first1=Alberto | last2=Katz | first2=Sheldon | authorlink2= Sheldon Katz | title=Lines on the Fermat quintic threefold and the infinitesimal generalized Hodge conjecture | jstor=2001512 | mr=1024767 | year=1991 | journal=Transactions of the American Mathematical Society | issn=0002-9947 | volume=324 | issue=1 | pages=353–368 | doi=10.2307/2001512}}
- {{Citation | last=Clemens | first=Herbert |authorlink= Herbert Clemens | title=Topics in transcendental algebraic geometry (Princeton, N.J., 1981/1982) | publisher=Princeton University Press | series=Annals of Mathematics Studies | mr=756858 | year=1984 | volume=106 | chapter=Some results about Abel-Jacobi mappings | pages=289–304}}
- {{Citation | last1=Cox | first1=David A. | authorlink1= David A. Cox | last2=Katz | first2=Sheldon | authorlink2= Sheldon Katz |title=Mirror symmetry and algebraic geometry | url=http://www.ams.org/bookstore-getitem/item=surv-68.s | publisher=American Mathematical Society | location=Providence, R.I. | series=Mathematical Surveys and Monographs | isbn=978-0-8218-1059-0 | mr=1677117 | year=1999 | volume=68}}
2 : 3-folds|Complex manifolds
- USS Staunch
- USS Staunch (AM-307)
- USS Staunch (MSF-307)
- USS St. Clair
- USS St. Clair (1862)
- USS STEADY
- USS Steady (AM-118)
- USS Steady (MSF-118)
- USS Steele
- USS Steele (DE-8)
- USS Stein
- USS Stein (DE-1065)
- USS Stennis
- U.S.S. Stennis
- USS Stentor (ARL-26)
- USS Stephen Potter
- USS Stephen Potter (DD 538)
- USS Stephen Young
- USS Stepping Stones
- USS Stepping Stones (1861)
- USS Sterett (CG-31)
- USS Sterett (DD-407)
- USS Sterett (DDG 104)
- USS Sterett (DLG-31)
- USS Stern