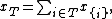“Folkman's theorem”的意思、由来-开放百科全书

词条

Folkman's theorem

释义

Statement of the theorem
Relation to Rado's theorem and Schur's theorem
Multiplication versus addition
Canonical Folkman Theorem
Previous results
References

Folkman's theorem is a theorem in mathematics, and more particularly in arithmetic combinatorics and Ramsey theory. According to this theorem, whenever the natural numbers are partitioned into finitely many subsets, there exist arbitrarily large sets of numbers all of whose sums belong to the same subset of the partition.^[1] The theorem had been discovered and proved independently by several mathematicians,^[2]^[3] before it was named "Folkman's theorem", as a memorial to Jon Folkman, by Graham, Rothschild, and Spencer.^[1]

Statement of the theorem

Let N be the set {1, 2, 3, ...} of positive integers, and suppose that N is partitioned into k different subsets N₁, N₂, ... N_k, where k is any positive integer. Then Folkman's theorem states that, for every positive integer m, there exists a set S_m and an index i_m such that S_m has m elements and such that every sum of a nonempty subset of S_m belongs to N_{i_m}.^[1]

Relation to Rado's theorem and Schur's theorem

Schur's theorem in Ramsey theory states that, for any finite partition of the positive integers, there exist three numbers x, y, and x + y that all belong to the same partition set. That is, it is the special case m = 2 of Folkman's theorem.

Rado's theorem in Ramsey theory concerns a similar problem statement in which the integers are partitioned into finitely many subsets; the theorem characterizes the integer matrices A with the property that the system of linear equations {{nowrap|1=A x = 0}} can be guaranteed to have a solution in which every coordinate of the solution vector x belongs to the same subset of the partition. A system of equations is said to be regular whenever it satisfies the conditions of Rado's theorem; Folkman's theorem is equivalent to the regularity of the system of equations

where T ranges over each nonempty subset of the set {{nowrap|{1, 2, ..., m}.}}^[1]

Multiplication versus addition

It is possible to replace addition by multiplication in Folkman's theorem: if the natural numbers are finitely partitioned, there exist arbitrarily large sets S such that all products of nonempty subsets of S belong to a single partition set. Indeed, if one restricts S to consist only of powers of two, then this result follows immediately from the additive version of Folkman's theorem. However, it is open whether there exist arbitrarily large sets such that all sums and all products of nonempty subsets belong to a single partition set. It is not even known whether there must necessarily exist a set of the form {{nowrap|{x, y, x + y, xy}}} for which all four elements belong to the same partition set.^[1]

Canonical Folkman Theorem

Let 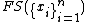denote the set of all finite sums of elements of 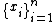. Let be a (possibly infinite) coloring of the positive integers, and let be an arbitrary positive integer. There exists 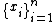such that at least one of the following 3 conditions holds.

1) 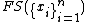is a monochromatic set.

2) 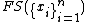is a rainbow set.

3) For any 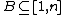, the color of 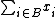is determined solely by .

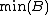Previous results

Variants of Folkman's theorem had been proved by Richard Rado and by J. H. Sanders.^[2]^[3] Folkman's theorem was named in memory of Jon Folkman by Ronald Graham, Bruce Lee Rothschild, and Joel Spencer, in their book on Ramsey theory.^[1]

References

1. ^¹²³⁴⁵{{citation|title=Ramsey Theory|first1=Ronald L.|last1=Graham|author1-link=Ronald Graham|first2=Bruce L.|last2=Rothschild|author2-link=Bruce Lee Rothschild|first3=Joel H.|last3=Spencer|author3-link=Joel Spencer|publisher=Wiley-Interscience|year=1980|contribution=3.4 Finite sums and finite unions (Folkman's theorem)|pages=65–69}}.
2. ^¹{{citation | last = Rado | first = R. | authorlink = Richard Rado | contribution = Some partition theorems | mr=297585 | location = Amsterdam | pages = 929–936 | publisher = North-Holland | title = Combinatorial theory and its applications, III: Proc. Colloq., Balatonfüred, 1969 | year = 1970}}.
3. ^¹{{citation | last = Sanders | first = Jon Henry |mr = 2617864 | publisher = Yale University | series = Ph.D. thesis | title = A generalization of Schur's theorem | year = 1968}}.

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。