请输入您要查询的百科知识：

　

词条 Fourier shell correlation
释义

  1. Calculation

  2. See also

  3. Notes

  4. References

  5. External links

In structural biology, as well as in virtually all sciences that produce three-dimensional data, the Fourier shell correlation (FSC) measures the normalised cross-correlation coefficient between two 3-dimensional volumes over corresponding shells in Fourier space (i.e., as a function of spatial frequency[1]). The FSC is the three-dimensional extension of the two-dimensional Fourier ring correlation (FRC);[2] also known as: spatial frequency correlation function.[3]

Calculation

where 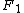is the complex structure Factor for volume 1, 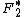is the complex conjugate of the structure Factor for volume 2, and is the individual voxel element at radius .[4][5][6] In this form, the FSC takes two three-dimensional data sets and converts them into a one-dimensional array.

The FSC originated in cryo-electron microscopy and gradually proliferated to other fields. To measure the FSC, two independently determined 3D volumes are required. In cryo-electron microscopy, the two volumes are the result of two three-dimensional reconstructions, each based on half of the available data set. Typically, the even particle images form one half and the odd particles the other half of the data set. Some publications quote the FSC 0.5 resolution cutoff, which ad hoc criterion refers to when the correlation coefficient of the Fourier shells is equal to 0.5.[7][8] However, determining the resolution threshold remains a controversial issue: fixed-value thresholds have been argued to be based on incorrect statistical assumptions.[6] Many other criteria using the FSC curve exist, including 3-σ criterion, 5-σ criterion, and the 0.143 cutoff. The half-bit criterion indicates at which resolution we have collected enough information to reliably interpret the 3-dimensional volume, and the (modified) 3-sigma criterion indicates where the FSC systematically emerges above the expected random correlations of the background noise.[6] The FSC 0.143 cutoff was proposed in part to make the resolution measurement comparable to measurements used in X-ray crystallography.[9] Currently, the 0.143 cutoff is the most commonly used criterion for the resolution of cryo-EM reconstructions better than 10 ångström resolution.[10] Fixed-value thresholds have, however, been refuted using elementary statistical counter examples; they will thus slowly disappear from the literature again in favour of reproducible resolution metrics.[11]

See also

  • Resolution (electron density)

Notes

1. ^Harauz & van Heel, 1986
2. ^van Heel, 1982
3. ^Saxton & Baumeister, 1982
4. ^{{cite web | title=Image Science's FSC: Program to calculate the Fourier Shell Correlation (FSC) of two 3D volumes | url=http://www.imagescience.de/fsc/ | work=fsc | publisher=Image Science | accessdate=2009-04-09}}
5. ^{{cite web | title=RF 3 - Phase Residual & Fourier shell correlation | url=http://www.wadsworth.org/spider_doc/spider/docs/man/rf3.html | work=SPIDER | publisher=Wadsworth Center | accessdate=2009-04-09}}
6. ^1 2 van Heel & Schatz, 2005
7. ^Böttcher et al., 1997
8. ^Frank, 2006, p250-251
9. ^Rosenthal & Henderson, 2003
10. ^{{Cite web|url=https://www.ebi.ac.uk/pdbe/emdb/|title=The Electron Microscopy Data Bank|website=www.ebi.ac.uk|access-date=2019-01-07}}
11. ^van Heel & Schatz, 2017

References

{{refbegin}}
  • {{cite journal

| last = Harauz
| first = G.
| author2= van Heel M.
| title = Exact filters for general geometry three dimensional reconstruction
| journal = Optik
| volume = 73
| pages = 146–156
| year = 1986}}
  • {{cite book

| last = van Heel
| first = M.
|author2= Keegstra, W.|author3= Schutter, W.|author4= van Bruggen E.F.J.
| title = Arthropod hemocyanin studies by image analysis, in: Structure and Function of Invertebrate Respiratory Proteins,EMBO Workshop 1982, E.J. Wood
| journal = Life Chemistry Reports
| volume = Suppl. 1
| pages = 69–73
| year = 1982
| isbn = 9783718601554}}
  • {{cite journal

| last = Saxton
| first = W.O.
|author2=W. Baumeister
| title = The correlation averaging of a regularly arranged bacterial cell envelope protein
| journal = Journal of Microscopy
| volume = 127
| pages = 127–138
| year = 1982
| doi = 10.1111/j.1365-2818.1982.tb00405.x
| issue = 2}}
  • {{cite journal

| last = Böttcher
| first = B.
|author2= Wynne, S.A.|author3=Crowther, R.A.
| title = Determination of the fold of the core protein of hepatitis B virus by electron microscopy
| journal = Nature
| volume = 386
| pages = 88–91
| doi=10.1038/386088a0
| year = 1997
| pmid = 9052786
| issue = 6620}}
  • {{cite journal

| title=Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy
| journal=Journal of Molecular Biology
| year= 2003
| volume= 333
| pages= 721–745
| last= Rosenthal
| first= P.B.
|author2=Henderson, R.
| ISSN= 0022-2836
| pmid= 14568533
| issue=4 }}
  • {{cite journal

| title=Fourier shell correlation threshold criteria
| journal=Journal of Structural Biology
| year= 2005
| last= van Heel
| first= M.
|author2=Schatz, M.
| volume=151
| pages=250–262
| doi=10.1016/j.jsb.2005.05.009
| pmid=16125414
| issue=3 }}
  • {{cite book

| last = Frank
| first = J.
| authorlink = Joachim Frank
| title = Three-Dimensional Electron Microscopy of Macromolecular Assemblies
| publisher = Oxford University Press
| location = New York
| year = 2006
| pages =
| isbn = 0-19-518218-9 }}
  • {{cite journal

| title=Reassessing the Revolution's Resolution
| journal=BioRxiv
| year= 2017
| last= van Heel
| first= M.
|author2=Schatz, M.
| doi=10.1101/224402{{refend}}

External links

  • EMstats Trends and distributions of maps in EM Data Bank (EMDB), e.g. resolution trends
{{DEFAULTSORT:Fourier Shell Correlation}}

1 : Applied mathematics
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/13 10:20:41