请输入您要查询的百科知识：

　

词条 Free convolution
释义

  1. Free additive convolution

  2. Rectangular free additive convolution

  3. Free multiplicative convolution

  4. Applications of free convolution

  5. See also

  6. References

  7. External links

Free convolution is the free probability analog of the classical notion of convolution of probability measures. Due to the non-commutative nature of free probability theory, one has to talk separately about additive and multiplicative free convolution, which arise from addition and multiplication of free random variables (see below; in the classical case, what would be the analog of free multiplicative convolution can be reduced to additive convolution by passing to logarithms of random variables). These operations have some interpretations in terms of empirical spectral measures of random matrices.[1]

The notion of free convolution was introduced by Voiculescu.[2][3]

Free additive convolution

Let and be two probability measures on the real line, and assume that is a random variable in a non commutative probability space with law and is a random variable in the same non commutative probability space with law . Assume finally that and are freely independent. Then the free additive convolution 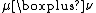is the law of . Random matrices interpretation: if and are some independent by Hermitian (resp. real symmetric) random matrices such that at least one of them is invariant, in law, under conjugation by any unitary (resp. orthogonal) matrix and such that the empirical spectral measures of and tend respectively to and as tends to infinity, then the empirical spectral measure of 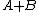tends to 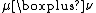.[4]

In many cases, it is possible to compute the probability measure 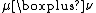explicitly by using complex-analytic techniques and the R-transform of the measures and .

Rectangular free additive convolution

The rectangular free additive convolution (with ratio ) 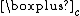has also been defined in the non commutative probability framework by Benaych-Georges[5] and admits the following random matrices interpretation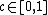. For , for and are some independent by complex (resp. real) random matrices such that at least one of them is invariant, in law, under multiplication on the left and on the right by any unitary (resp. orthogonal) matrix and such that the empirical singular values distribution of and tend respectively to and as and tend to infinity in such a way that 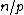tends to , then the empirical singular values distribution of 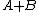tends to 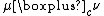.[6]

In many cases, it is possible to compute the probability measure 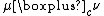explicitly by using complex-analytic techniques and the rectangular R-transform with ratio of the measures and .

Free multiplicative convolution

Let and be two probability measures on the interval 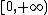, and assume that is a random variable in a non commutative probability space with law and is a random variable in the same non commutative probability space with law . Assume finally that and are freely independent. Then the free multiplicative convolution 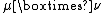is the law of 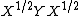(or, equivalently, the law of 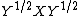. Random matrices interpretation: if and are some independent by non negative Hermitian (resp. real symmetric) random matrices such that at least one of them is invariant, in law, under conjugation by any unitary (resp. orthogonal) matrix and such that the empirical spectral measures of and tend respectively to and as tends to infinity, then the empirical spectral measure of tends to 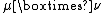.[7]

A similar definition can be made in the case of laws 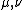supported on the unit circle 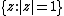, with an orthogonal or unitary random matrices interpretation.

Explicit computations of multiplicative free convolution can be carried out using complex-analytic techniques and the S-transform.

Applications of free convolution

  • Free convolution can be used to give a proof of the free central limit theorem.
  • Free convolution can be used to compute the laws and spectra of sums or products of random variables which are free. Such examples include: random walk operators on free groups (Kesten measures); and asymptotic distribution of eigenvalues of sums or products of independent random matrices.

Through its applications to random matrices, free convolution has some strong connections with other works on G-estimation of Girko.

The applications in wireless communications, finance and biology have provided a useful framework when the number of observations is of the same order as the dimensions of the system.

See also

  • Convolution
  • Free probability
  • Random matrix

References

1. ^Anderson, G.W.; Guionnet, A.; Zeitouni, O. (2010). An introduction to random matrices. Cambridge: Cambridge University Press. {{isbn|978-0-521-19452-5}}.
2. ^Voiculescu, D., Addition of certain non-commuting random variables, J. Funct. Anal. 66 (1986), 323–346
3. ^Voiculescu, D., Multiplication of certain noncommuting random variables, J. Operator Theory 18 (1987), 2223–2235
4. ^Anderson, G.W.; Guionnet, A.; Zeitouni, O. (2010). An introduction to random matrices. Cambridge: Cambridge University Press. {{isbn|978-0-521-19452-5}}.
5. ^Benaych-Georges, F., Rectangular random matrices, related convolution, Probab. Theory Related Fields Vol. 144, no. 3 (2009) 471-515.
6. ^Benaych-Georges, F., Rectangular random matrices, related convolution, Probab. Theory Related Fields Vol. 144, no. 3 (2009) 471-515.
7. ^Anderson, G.W.; Guionnet, A.; Zeitouni, O. (2010). An introduction to random matrices. Cambridge: Cambridge University Press. {{isbn|978-0-521-19452-5}}.
  • "Free Deconvolution for Signal Processing Applications", O. Ryan and M. Debbah, ISIT 2007, pp. 1846–1850
  • James A. Mingo, Roland Speicher: [//www.springer.com/us/book/9781493969418 Free Probability and Random Matrices]. Fields Institute Monographs, Vol. 35, Springer, New York, 2017.
  • D.-V. Voiculescu, N. Stammeier, M. Weber (eds.): Free Probability and Operator Algebras, Münster Lectures in Mathematics, EMS, 2016

External links

  • Alcatel Lucent Chair on Flexible Radio
  • http://www.cmapx.polytechnique.fr/~benaych
  • http://folk.uio.no/oyvindry
  • [https://www.math.uni-sb.de/ag/speicher/speicher_publikationenE.html survey articles] of Roland Speicher on free probability.

5 : Signal processing|Combinatorics|Functional analysis|Free probability theory|Free algebraic structures
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 6:41:16