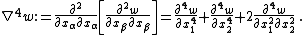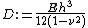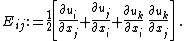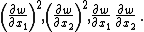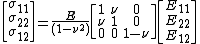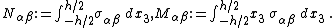- Validity of the Föppl–von Kármán equations
- Equations in terms of Airy stress function
- Pure bending
- Kinematic assumptions (Kirchhoff hypothesis)
- Strain-displacement relations (von Kármán strains)
- Stress–strain relations
- Stress resultants
- Föppl–von Kármán equations in terms of stress resultants
- References
- See also
The Föppl–von Kármán equations, named after August Föppl[1] and Theodore von Kármán,[2] are a set of nonlinear partial differential equations describing the large deflections of thin flat plates.[3] With applications ranging from the design of submarine hulls to the mechanical properties of cell wall,[4] the equations are notoriously difficult to solve, and take the following form:
[5]where {{math|E}} is the Young's modulus of the plate material (assumed homogeneous and isotropic), {{math|υ}} is the Poisson's ratio, {{math|h}} is the thickness of the plate, {{math|w}} is the out–of–plane deflection of the plate, {{math|P}} is the external normal force per unit area of the plate, {{math|σαβ}} is the Cauchy stress tensor, and {{math|α, β}} are indices that take values of 1 and 2 (the two orthogonal in-plane directions). The 2-dimensional biharmonic operator is defined as[6]
Equation (1) above can be derived from kinematic assumptions and the constitutive relations for the plate. Equations (2) are the two equations for the conservation of linear momentum in two dimensions where it is assumed that the out–of–plane stresses ({{math|σ33,σ13,σ23}}) are zero.
Validity of the Föppl–von Kármán equations
While the Föppl–von Kármán equations are of interest from a purely mathematical point of view, the physical validity of these equations is questionable.[7] Ciarlet[8] states: The two-dimensional von Karman equations for plates, originally proposed by von Karman [1910], play a mythical role in applied mathematics. While they have been abundantly, and satisfactorily, studied from the mathematical standpoint, as regards notably various questions of existence, regularity, and bifurcation, of their solutions, their physical soundness has been often seriously questioned. Reasons include the facts that
- the theory depends on an approximate geometry which is not clearly defined
- a given variation of stress over a cross-section is assumed arbitrarily
- a linear constitutive relation is used that does not correspond to a known relation between well defined measures of stress and strain
- some components of strain are arbitrarily ignored
- there is a confusion between reference and deformed configurations which makes the theory inapplicable to the large deformations for which it was apparently devised.
Conditions under which these equations are actually applicable and will give reasonable results when solved are discussed in Ciarlet.[8][9]
Equations in terms of Airy stress function
The three Föppl–von Kármán equations can be reduced to two by introducing the Airy stress function  where
where
Then the above equations become[5]
Pure bending
For the pure bending of thin plates the equation of equilibrium is 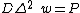 , where
, where
is called flexural or cylindrical rigidity of the plate.[5]
Kinematic assumptions (Kirchhoff hypothesis)
In the derivation of the Föppl–von Kármán equations the main kinematic assumption (also known as the Kirchhoff hypothesis) is that surface normals to the plane of the plate remain perpendicular to the plate after deformation. It is also assumed that the in-plane (membrane) displacements are small and the change in thickness of the plate is negligible. These assumptions imply that the displacement field {{math|u}} in the plate can be expressed as[10]
in which {{math|v}} is the in-plane (membrane) displacement. This form of the displacement field implicitly assumes that the amount of rotation of the plate is small.
Strain-displacement relations (von Kármán strains)
The components of the three-dimensional Lagrangian Green strain tensor are defined as
Substitution of the expressions for the displacement field into the above gives
For small strains but moderate rotations, the higher order terms that cannot be neglected are
Neglecting all other higher order terms, and enforcing the requirement that the plate does not change its thickness, the strain tensor components reduce to the von Kármán strains
Stress–strain relations
If we assume that the Cauchy stress tensor components are linearly related to the von Kármán strains by Hooke's law, the plate is isotropic and homogeneous, and that the plate is under a plane stress condition,[11] we have {{math|σ33}} = {{math|σ13}} = {{math|σ23}} = 0 and
Expanding the terms, the three non-zero stresses are
Stress resultants
The stress resultants in the plate are defined as
Therefore,
and
Solutions are easier to find when the governing equations are expressed in terms of stress resultants rather than the in-plane stresses.
Föppl–von Kármán equations in terms of stress resultants
The Föppl–von Kármán equations are typically derived with an energy approach by considering variations of internal energy and the virtual work done by external forces. A similar approach can be used to write these equations in terms of stress resultants. The resulting governing equations are
References
2. ^von Kármán, T., "Festigkeitsproblem im Maschinenbau," Encyk. D. Math. Wiss. IV, 311–385 (1910)
3. ^E. Cerda and L. Mahadevan, 2003, "Geometry and Physics of Wrinkling" Phys. Rev. Lett. 90, 074302 (2003)
4. ^http://focus.aps.org/story/v27/st6
5. ^1 2 "Theory of Elasticity". L. D. Landau, E. M. Lifshitz, (3rd ed. {{ISBN|0-7506-2633-X}})
6. ^The 2-dimensional Laplacian, {{math|Δ}}, is defined as
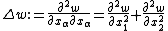
7. ^von Karman plate equations http://imechanica.org/node/6618 Accessed Tue July 30 2013 14:20.
8. ^1 {{Citation|last=Ciarlet|first=P. G.|year=1990|title=Plates and Junctions in Elastic Multi-Structures|publisher=Springer-Verlag.}}
9. ^{{Citation|last= Ciarlet|first= Philippe G. | title=A justification of the von Kármán equations|journal= Archive for Rational Mechanics and Analysis |volume=73|year=1980|pages= 349–389.|issue=4|bibcode= 1980ArRMA..73..349C|doi= 10.1007/BF00247674}}
10. ^{{Citation|last= Ciarlet|first= Philippe G. | title=A justification of the von Kármán equations|journal= Archive for Rational Mechanics and Analysis |volume=73|year=1980|pages= 349–389.|issue=4|bibcode= 1980ArRMA..73..349C|doi= 10.1007/BF00247674}}
11. ^Typically, an assumption of zero out-of-plane stress is made at this point.
See also
- Plate theory
- John Hamtramck
- John Hanamaker
- John Hanboys
- John Hanbury
- John Hanbury (1664-1734)
- John Hanbury (1664–1734)
- John Hanbury (1744-1784)
- John Hanbury (disambiguation)
- John Hanbury Martin
- John Hance
- John Hancock (actor)
- John Hancock (film director)
- John Hancock Life Insurance
- John Hancock Observatory
- John Hancock (radio host)
- John Hancock Student Village
- John Hancock Warehouse
- John Hand Building
- John Handcock (Ballyshannon MP)
- John Handcock (disambiguation)
- John Handcock (Philipstown MP)
- John Handcock (politician)
- John Handcox
- John Handegard
- John H. Anderson