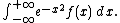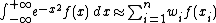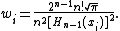“Gauss–Hermite quadrature”的意思、由来-开放百科全书

词条

Gauss–Hermite quadrature

释义

Example with change of variable
References
External links

In numerical analysis, Gauss–Hermite quadrature is a form of Gaussian quadrature for approximating the value of integrals of the following kind:

In this case

where n is the number of sample points used. The x_i are the roots of the physicists' version of the Hermite polynomial H_n(x) (i = 1,2,...,n), and the associated weights w_i are given by

^[1]

Example with change of variable

Let's consider a function h(y), where the variable y is Normally distributed: 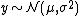. The expectation of h corresponds to the following integral:

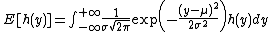
As this doesn't exactly correspond to the Hermite polynomial, we need to change variables:

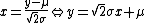
Coupled with the integration by substitution, we obtain:

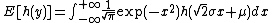
leading to:

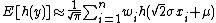
References

1. ^Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, {{ISBN|978-0-486-61272-0}}. Equation 25.4.46.

* {{dlmf| id = 3.5.E28| title=Quadrature: Gauss–Hermite Formula}}

{{cite journal|first1=T. S. | last1=Shao | first2=T. C. | last2=Chen | first3= R. M. | last3=Frank

|title=Tables of zeros and Gaussian weights of certain associated Laguerre polynomials and the related generalized Hermite polynomials
|year=1964
|journal=Math. Comp. | mr=0166397 | volume=18 | number=88 | pages=598–616 |doi=10.1090/S0025-5718-1964-0166397-1}}

{{cite journal|first1=N. M. | last1=Steen | first2=G. D. | last2=Byrne

|first3=E. M. | last3=Gelbard | title = Gaussian quadratures for the integrals

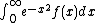and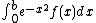

|journal = Math. Comp. | year=1969
|volume=23 | number=107 | pages=661–671 | mr=0247744 | doi=10.1090/S0025-5718-1969-0247744-3 }}

{{cite journal|first1= B. | last1=Shizgal | title = A Gaussian quadrature procedure for use in the solution of the Boltzmann equation and related problems

|journal=J. Comput. Phys. | volume=41 | pages=309–328 | year=1981
|doi=10.1016/0021-9991(81)90099-1 }}

External links

For tables of Gauss-Hermite abscissae and weights up to order n = 32 see http://www.efunda.com/math/num_integration/findgausshermite.cfm.
Generalized Gauss–Hermite quadrature, free software in C++, Fortran, and Matlab

1 : Numerical integration (quadrature)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。