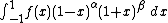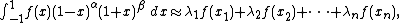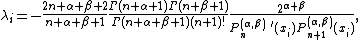“Gauss–Jacobi quadrature”的意思、由来-开放百科全书

词条

Gauss–Jacobi quadrature

释义

References
External links

In numerical analysis, Gauss–Jacobi quadrature (named after Carl Friedrich Gauss and Carl Gustav Jacob Jacobi) is a method of numerical quadrature based on Gaussian quadrature. Gauss–Jacobi quadrature can be used to approximate integrals of the form

where ƒ is a smooth function on [−1, 1] and α, β > −1. The interval [−1, 1] can be replaced by any other interval by a linear transformation. Thus, Gauss–Jacobi quadrature can be used to approximate integrals with singularities at the end points. Gauss–Legendre quadrature is a special case of Gauss–Jacobi quadrature with α = β = 0. Similarly, the Chebyshev–Gauss quadrature of the first (second) kind arises when one takes α = β = -0.5 (+0.5). More generally, the special case α = β turns Jacobi polynomials into Gegenbauer polynomials, in which case the technique is sometimes called Gauss–Gegenbauer quadrature.

Gauss–Jacobi quadrature uses ω(x) = (1 − x)^α (1 + x)^β as the weight function. The corresponding sequence of orthogonal polynomials consist of Jacobi polynomials. Thus, the Gauss–Jacobi quadrature rule on n points has the form

where x₁, …, x_n are the roots of the Jacobi polynomial of degree n. The weights λ₁, …, λ_n are given by the formula

where Γ denotes the Gamma function and {{math|P{{su|b=n|p=(α, β)}}(x)}} the Jacobi polynomial of degree n.

References

{{Citation | last1=Rabinowitz | first1=Philip | author1-link=Philip Rabinowitz (mathematician) | title=A First Course in Numerical Analysis | publisher=Dover Publications | location=New York | edition=2nd | isbn=978-0-486-41454-6 | year=2001 | chapter=§4.8-1: Gauss–Jacobi quadrature}}.

External links

Jacobi rule - free software (Matlab, C++, and Fortran) to evaluate integrals by Gauss–Jacobi quadrature rules.
Gegenbauer rule - free software (Matlab, C++, and Fortran) for Gauss–Gegenbauer quadrature

1 : Numerical integration (quadrature)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。