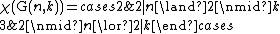请输入您要查询的百科知识：

　

词条 Generalized Petersen graph
释义

  1. Definition and notation

  2. Examples

  3. Properties

     Isomorphisms  Girth  Chromatic number and chromatic index 

  4. References

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter[1] and was given its name in 1969 by Mark Watkins.[2]

Definition and notation

In Watkins' notation, G(n,k) is a graph

with vertex set

{u0, u1, ..., un−1, v0, v1, ..., vn−1}

and edge set

{ui ui+1, ui vi, vi vi+k: i = 0,...,n − 1}

where subscripts are to be read modulo n and k < n/2. Some authors use a similar notation GPG(n,k) with the same meaning.Coxeter's notation for the same graph would be {n}+{n/k}, a combination of the Schläfli symbols for the regular n-gon and star polygon from which the graph is formed.

Any generalized Petersen graph can also be constructed from a voltage graph with two vertices, two self-loops, and one other edge.[3]

The Petersen graph itself is G(5,2) or {5}+{5/2}.

Examples

Among the generalized Petersen graphs are the n-prism G(n,1), the Dürer graph G(6,2), the Möbius-Kantor graph G(8,3), the dodecahedron G(10,2), the Desargues graph G(10,3) and the Nauru graph G(12,5).

Four generalized Petersen graphs – the 3-prism, the 5-prism, the Dürer graph, and G(7,2) – are among the seven graphs that are cubic, 3-vertex-connected, and well-covered (meaning that all of their maximal independent sets have equal size).[4]

Properties

This family of graphs possesses a number of interesting properties. For example,

  1. G(n,k) is vertex-transitive (meaning that it has symmetries that take any vertex to any other vertex) if and only if n = 10 and k =2 or if k2 ≡ ±1 (mod n).
  2. It is edge-transitive (having symmetries that take any edge to any other edge) only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5).&91;5&93; These seven graphs are therefore the only symmetric generalized Petersen graphs.
  3. It is bipartite if and only if n is even and k is odd.
  4. It is a Cayley graph if and only if k2 ≡ 1 (mod n).
  5. It is hypohamiltonian when n is congruent to 5 modulo 6 and k is 2, n−2, (n+1)/2, or (n−1)/2 (all four of these choices of k lead to isomorphic graphs). It is also non-Hamiltonian when n is divisible by four, at least equal to 8, and k is n/2. In all other cases it has a Hamiltonian cycle.&91;6&93; When n is congruent to 3 modulo 6 and k is 2, G(n,k) has exactly three Hamiltonian cycles.&91;7&93; For G(n,2), the number of Hamiltonian cycles can be computed by a formula that depends on the congruence class of n modulo six and involves the Fibonacci numbers.&91;8&93;

Every generalized Petersen graph is a unit distance graph.[9]

Isomorphisms

G(n,k) is isomorphic to G(n,l) if and only if kl ≡ 1 (mod n).[10]

Girth

The girth of a generalized Petersen graph, g(G(n,k)) is at least 3 and at most 8, in particular G(PG(n,k)) ≤ .[11]

A table with exact girth values:

Condition Girth
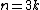3
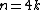4
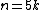5
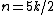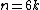6
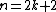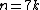7
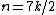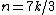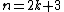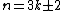otherwise 8

Chromatic number and chromatic index

Being regular, according to Brooks' theorem their chromatic number can not be larger than their degree. Generalized Petersen graphs are cubic, so their chromatic number can be either 2 or 3. More exactly:

Where denotes the logical AND, while the logical OR. For example, the chromatic number of 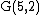is 3.

Petersen graph, being a snark, has a chromatic index of 4. All other generalized Petersen graph has chromatic index 3.[12]

The generalized Petersen graph G(9,2) is one of the few graphs known to have only one 3-edge-coloring.[13]

The Petersen graph itself is the only generalized Petersen graph that is not 3-edge-colorable.[14]

References

1. ^{{citation | last = Coxeter | first = H. S. M. | author-link = Harold Scott MacDonald Coxeter | doi = 10.1090/S0002-9904-1950-09407-5 | journal = Bulletin of the American Mathematical Society | pages = 413–455 | title = Self-dual configurations and regular graphs | volume = 56 | year = 1950}}.
2. ^{{citation | last = Watkins | first = Mark E. | doi = 10.1016/S0021-9800(69)80116-X | journal = Journal of Combinatorial Theory | pages = 152–164 | title = A Theorem on Tait Colorings with an Application to the Generalized Petersen Graphs | volume = 6 | year = 1969}}.
3. ^{{citation | last1 = Gross | first1 = Jonathan L. | last2 = Tucker | first2 = Thomas W. | location = New York | publisher = Wiley | title = Topological Graph Theory | year = 1987}}. Example 2.1.2, p.58.
4. ^{{citation | last1 = Campbell | first1 = S. R. | last2 = Ellingham | first2 = M. N. | author2-link = Mark Ellingham | last3 = Royle | first3 = Gordon F. | author3-link = Gordon Royle | journal = Journal of Combinatorial Mathematics and Combinatorial Computing | mr = 1220613 | pages = 193–212 | title = A characterisation of well-covered cubic graphs | volume = 13 | year = 1993}}.
5. ^{{citation | last1 = Frucht | first1 = R. | author1-link = R. Frucht | last2 = Graver | first2 = J. E. | last3 = Watkins | first3 = M. E. | doi = 10.1017/S0305004100049811 | journal = Proceedings of the Cambridge Philosophical Society | pages = 211–218 | title = The groups of the generalized Petersen graphs | volume = 70 | year = 1971}}.
6. ^{{citation | last = Alspach | first = B. R. | authorlink = Brian Alspach | doi = 10.1016/0095-8956(83)90042-4 | mr = 0714452 | journal = Journal of Combinatorial Theory, Series B | pages = 293–312 | title = The classification of Hamiltonian generalized Petersen graphs | volume = 34 | year = 1983}}.
7. ^{{citation|title=Cubic graphs with three Hamiltonian cycles are not always uniquely edge colorable|first=Andrew|last=Thomason|doi=10.1002/jgt.3190060218|journal=Journal of Graph Theory|volume=6|issue=2|year=1982|pages=219–221}}.
8. ^{{citation | last = Schwenk | first = Allen J. | doi = 10.1016/0095-8956(89)90064-6 | issue = 1 | journal = Journal of Combinatorial Theory | series = Series B | mr = 1007713 | pages = 53–59 | title = Enumeration of Hamiltonian cycles in certain generalized Petersen graphs | volume = 47 | year = 1989}}.
9. ^{{citation | last1 = Žitnik | first1 = Arjana | last2 = Horvat | first2 = Boris | last3 = Pisanski | first3 = Tomaž | author3-link = Tomaž Pisanski | series = IMFM preprints | title = All generalized Petersen graphs are unit-distance graphs | url = http://preprinti.imfm.si/PDF/01109.pdf | volume = 1109 | year = 2010}}.
10. ^{{citation|title=The isomorphism classes of the generalized Petersen graphs|first=Alice|last=Steimle|first2=William|last2=Staton|journal=Discrete Mathematics|volume=309|issue=1|year=2009|page=231–237 |doi=10.1016/j.disc.2007.12.074}}
11. ^{{Citation|url = http://danielaferrero.wp.txstate.edu/files/2015/03/Component-connectivity-generalized-Petersen-graphs.pdf |doi=10.1080/00207160.2013.878023 | journal=International Journal of Computer Mathematics | first1=Daniela | last1=Ferrero | first2=Sarah | last2=Hanusch | page=1940–1963 | volume=91 | issue=9 | year=2014 |title= Component connectivity of generalized Petersen graphs | issn=0020-7160}}
12. ^{{citation | last1 = Castagna | first1 = Frank | last2 = Prins | first2 = Geert Caleb Ernst | journal = Pacific Journal of Mathematics | title = Every generalized Petersen graph has a Tait coloring | volume = 40 | issue = 1 | year = 1972 | doi = 10.2140/pjm.1972.40.53|issn=0030-8730|mr=304223|zbl=0236.05106}}
13. ^{{citation|first=Béla|last=Bollobás|authorlink=Béla Bollobás|title=Extremal Graph Theory|publisher=Dover|year=2004|page=233}}. Reprint of 1978 Academic Press edition.
14. ^{{citation | last1 = Castagna | first1 = Frank | last2 = Prins | first2 = Geert | journal = Pacific Journal of Mathematics | title = Every Generalized Petersen Graph has a Tait Coloring | volume = 40 | year = 1972 | doi = 10.2140/pjm.1972.40.53 }}.

2 : Parametric families of graphs|Regular graphs
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/9/30 16:37:03