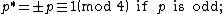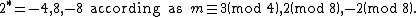- See also
- References
In algebraic number theory, the genus field G of an algebraic number field K is the maximal abelian extension of K which is obtained by composing an absolutely abelian field with K and which is unramified at all finite primes of K. The genus number of K is the degree [G:K] and the genus group is the Galois group of G over K.
If K is itself absolutely abelian, the genus field may be described as the maximal absolutely abelian extension of K unramified at all finite primes: this definition was used by Leopoldt and Hasse.
If K=Q({{radic|m}}) (m squarefree) is a quadratic field of discriminant D, the genus field of K is a composite of quadratic fields. Let pi run over the prime factors of D. For each such prime p, define p∗ as follows:
Then the genus field is the composite 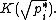
See also
- Hilbert class field
References
- {{cite book | last=Ishida | first=Makoto | title=The genus fields of algebraic number fields | series=Lecture Notes in Mathematics | volume=555 | publisher=Springer-Verlag | year=1976 | isbn=3-540-08000-7 | zbl=0353.12001 }}
- {{cite book | first=Gerald | last=Janusz | title=Algebraic Number Fields | year=1973 | publisher=Academic Press | isbn=0-12-380250-4 | series=Pure and Applied Mathematics | volume=55 | zbl=0307.12001 }}
- {{cite book | last=Lemmermeyer | first= Franz | title=Reciprocity laws. From Euler to Eisenstein | series= Springer Monographs in Mathematics | publisher=Springer-Verlag | location=Berlin | year= 2000 | isbn= 3-540-66957-4 | url=https://books.google.com/books?id=EwjpPeK6GpEC | mr=1761696 | zbl=0949.11002 }}
- Santa Fe, NM
- Santa Fe, Nueva Vizcaya
- Santa Fe, Ocotepeque
- Santa Fe Opera
- Santa Fe Pacific Corporation
- Santa Fe, Panama
- Santa Fe Province
- Santa Fe (province)
- Santa Fe Province, Argentina
- Santa Fe Railroad
- Santa Fe Regional Airport
- Santa Fe, Romblon
- Santa Fe Springs
- Santa Fe Springs, CA
- Santa Fe Springs, California
- Santa Fe Swamp
- Santa Fe, Texas
- Santa Fe Trail
- Santa Fe, TX
- Santa Fe University of Art and Design
- Santa Fe–Southern Pacific merger
- Santa Fé
- Santa Fé, Argentina
- Santa Fé de Bogotá
- Santa Fé (football)