1. Basic definition

2. Types of modules

3. Operations on modules
     Changing scalars  

4. Homological algebra

5. Modules over special rings

6. Miscellaneous

7. See also

8. References

Module theory is the branch of mathematics in which modules are studied. This is a glossary of some terms of the subject.

Basic definition

left R-module

A left module over the ring is an abelian group with an operation (called scalar multipliction) satisfies the following condition:

,

right R-module

A right module over the ring is an abelian group with an operation satisfies the following condition:

,

Or it can be defined as the left module over (the opposite ring of ).

//bimodule">bimodule

If an abelian group is both a left -module and right -module, it can be made to a -bimodule if .

//submodule">submodule

Given is a left -module, a subgroup of is a submodule if .

homomorphism of -modules

For two left -modules , a group homomorphism is called homomorphism of -modules if .

//quotient module">quotient module

Given a left -modules , a submodule , can be made to a left -module by . It is also called a factor module.

//annihilator (ring theory)">annihilator

The annihilator of a left -module is the set . It is a (left) ideal of .

The annihilator of an element is the set .

Types of modules

//finitely generated module">finitely generated module

A module is finitely generated if there exist finitely many elements in such that every element of is a finite linear combination of those elements with coefficients from the scalar ring .

//cyclic module">cyclic module

A module is called a cyclic module if it is generated by one element.

//free module">free module

A free module is a module that has a basis, or equivalently, one that is isomorphic to a direct sum of copies of the scalar ring .

; basis

A basis of a module is a set of elements in such that every element in the module can be expressed as a finite sum of elements in the basis in a unique way.

//Projective module">Projective module

A -module is called a projective module if given a -module homomorphism , and a surjective -module homomorphism , there exists a -module homomorphism such that .

The following conditions are equivalent:

• The covariant functor 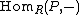is exact.
• is a projective module.
• Every short exact sequence is split.
• is a direct summand of free modules.

In particular, every free module is projective.

//injective module">injective module

A -module is called an injective module if given a -module homomorphism , and an injective -module homomorphism , there exists a

-module homomorphism 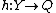such that .

The following conditions are equivalent:

• The contravariant functor is exact.
• is a injective module.
• Every short exact sequence is split.

//flat module">flat module

A -module is called a flat module if the tensor product functor is exact.

In particular, every projective module is flat.

//simple module">simple module

A simple module is a nonzero module whose only submodules are zero and itself.

//indecomposable module">indecomposable module

An indecomposable module is a non-zero module that cannot be written as a direct sum of two non-zero submodules. Every simple module is indecomposable.

//principal indecomposable module">principal indecomposable module

A cyclic indecomposable projective module is known as a PIM.

//semisimple module">semisimple module

A module is called semisimple if it is the direct sum of simple submodules.

//faithful module">faithful module

A faithful module is one where the action of each nonzero on is nontrivial (i.e. for some x in M). Equivalently, is the zero ideal.

//Noetherian module">Noetherian module

A Noetherian module is a module such that every submodule is finitely generated. Equivalently, every increasing chain of submodules becomes stationary after finitely many steps.

//Artinian module">Artinian module

An Artinian module is a module in which every decreasing chain of submodules becomes stationary after finitely many steps.

//finite length module">finite length module

A module which is both Artinian and Noetherian has additional special properties.

//graded module">graded module

A module over a graded ring is a graded module if can be expressed as a direct sum and .

//invertible module">invertible module

Roughly synonymous to rank 1 projective module.

//uniform module">uniform module

Module in which every two non-zero submodules have a non-zero intersection.

//algebraically compact module">algebraically compact module (pure injective module)

Modules in which all systems of equations can be decided by finitary means. Alternatively, those modules which leave pure-exact sequence exact after applying Hom.

//injective cogenerator">injective cogenerator

An injective module such that every module has a nonzero homomorphism into it.

//irreducible module">irreducible module

synonymous to "simple module"

//completely reducible module">completely reducible module

synonymous to "semisimple module"

Operations on modules

//Direct sum of modules">Direct sum of modules

//Tensor product of modules">Tensor product of modules

//Hom functor">Hom functor

//Ext functor">Ext functor

//Tor functor">Tor functor

//Essential extension">Essential extension

An extension in which every nonzero submodule of the larger module meets the smaller module in a nonzero submodule.

//Injective envelope">Injective envelope

A maximal essential extension, or a minimal embedding in an injective module

//Projective cover">Projective cover

A minimal surjection from a projective module.

//Socle (mathematics)">Socle

The largest semisimple submodule

//Radical of a module">Radical of a module

The intersection of the maximal submodules. For Artinian modules, the smallest submodule with semisimple quotient.

Changing scalars

//Restriction of scalars">Restriction of scalars

Uses a ring homomorphism from R to S to convert S-modules to R-modules

//Extension of scalars">Extension of scalars

Uses a ring homomorphism from R to S to convert R-modules to S-modules

//Localization of a module">Localization of a module

Converts R modules to S modules, where S is a localization of R

//Endomorphism ring">Endomorphism ring

A left R-module is a right S-module where S is its endomorphism ring.

Homological algebra

//Mittag-Leffler condition">Mittag-Leffler condition (ML)

//Short five lemma">Short five lemma

//Five lemma">Five lemma

//Snake lemma">Snake lemma

Modules over special rings

//D-module">D-module

A module over a ring of differential operators.

//Drinfeld module">Drinfeld module

A module over a ring of functions on algebraic curve with coefficients from a finite field.

//Galois module">Galois module

A module over the group ring of a Galois group

//Structure theorem for finitely generated modules over a principal ideal domain">Structure theorem for finitely generated modules over a principal ideal domain

Finitely generated modules over PIDs are finite direct sums of primary cyclic modules.

//Tate module">Tate module

A special kind of Galois module

Miscellaneous

//Rational canonical form">Rational canonical form

//elementary divisor">elementary divisor

//invariant (mathematics)">invariants

//fitting ideal">fitting ideal

normal forms for matrices

//Jordan Hölder composition series">Jordan Hölder composition series

//tensor product">tensor product

See also

• Glossary of ring theory

References

• {{cite book | author=John A. Beachy | title=Introductory Lectures on Rings and Modules | edition=1st | publisher=Addison-Wesley | year=1999 | isbn=0-521-64407-0 }}
• {{Citation | last1=Golan | first1=Jonathan S. | last2=Head | first2=Tom | title=Modules and the structure of rings | publisher=Marcel Dekker | series=Monographs and Textbooks in Pure and Applied Mathematics | isbn=978-0-8247-8555-0 |mr=1201818 | year=1991 | volume=147}}
• {{Citation | last1=Lam | first1=Tsit-Yuen | title=Lectures on modules and rings | publisher=Springer-Verlag | location=Berlin, New York | series=Graduate Texts in Mathematics No. 189 | isbn=978-0-387-98428-5 |mr=1653294 | year=1999}}
• {{cite book | author=Serge Lang | authorlink=Serge Lang | title=Algebra | edition=3rd | publisher=Addison-Wesley | year=1993 | isbn=0-201-55540-9 }}
• {{Citation | last1=Passman | first1=Donald S. | title=A course in ring theory | publisher=Wadsworth & Brooks/Cole Advanced Books & Software | location=Pacific Grove, CA | series=The Wadsworth & Brooks/Cole Mathematics Series | isbn=978-0-534-13776-2 |mr=1096302 | year=1991}}

• Psittacus eques
• Psittacus hollandicus
• Psittacus jandaya
• Psittacus luteus
• Psittacus madagascarensis
• Psittacus madagascariensis
• Psittacus mascarenus
• Psittacus mascarinus
• Psittacus monachus
• Psittacus obscurus
• Psittacus timneh
• Psittacus tricolor
• Psittacus violaceus
• Psittiparus
• Psittiparus bakeri
• Psittiparus gularis
• Psittiparus margaritae
• Psittiparus ruficeps
• Psittocosaurus
• Psittrichasiidae
• Psittrichasinae
• PS IV
• P. Sivakami
• P.Sivakozhundu
• P. Sivakozhundu