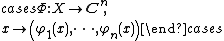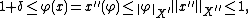“Goldstine theorem”的意思、由来-开放百科全书

词条

Goldstine theorem

释义

Proof
See also
References

In functional analysis, a branch of mathematics, the Goldstine theorem, named after Herman Goldstine, is stated as follows:

Goldstine theorem. Let {{mvar|X}} be a Banach space, then the image of the closed unit ball {{math|B ⊂ X}} under the canonical embedding into the closed unit ball {{math|B′′}} of the bidual space {{math|X ′′}} is weak*-dense.

The conclusion of the theorem is not true for the norm topology, which can be seen by considering the Banach space of real sequences that converge to zero, {{math|c₀}}, and its bi-dual space {{math|ℓ_∞}}.

Proof

Given {{math|x′′ ∈ B′′}}, an {{mvar|n}}-tuple {{math|(φ₁, ..., φ_n)}} of linearly independent elements of {{math|X ′}} and a {{math|δ > 0}} one shall find {{mvar|x}} in {{math|(1 + δ)B}} such that {{math|φ_i (x) {{=}} x′′(φ_i)}} for {{math|1 ≤ i ≤ n}}.

If the requirement {{math|{{!!}}x{{!!}} ≤ 1 + δ}} is dropped, the existence of such an {{mvar|x}} follows from the surjectivity of

Now let

Every element of {{math|(x + Y) ∩ (1 + δ)B}} has the required property, so that it suffices to show that the latter set is not empty.

Assume that it is empty. Then {{math|dist(x, Y) ≥ 1 + δ}} and by the Hahn–Banach theorem there exists a linear form {{math|φ ∈ X ′}} such that {{math|φ{{!}}_Y {{=}} 0, φ(x) ≥ 1 + δ}} and {{math|{{!!}}φ{{!!}}_X ′ {{=}} 1}}. Then {{math|φ ∈ span{φ₁, ..., φ_n},}} and therefore

which is a contradiction.

References

{{Functional Analysis}}Schwach-*-Topologie#Eigenschaften

2 : Banach spaces|Theorems in functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Proof

See also

References