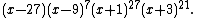- Construction
- Properties
- References
- External links
| image =
| image_caption = Gosset graph (321)
(There are 3 rings of 18 vertices, and two vertices coincide in the center of this projection. Edges also coincide with this projection.)
| name = Gosset graph
| namesake = Thorold Gosset
| vertices = 56
| edges = 756
| automorphisms = 2903040
| diameter = 3
| radius = 3
| girth = 3
| properties = Distance-regular graph
Integral
Vertex-transitive
}}
The Gosset graph, named after Thorold Gosset, is a specific regular graph (1-skeleton of the 7-dimensional 321 polytope) with 56 vertices and valency 27.[1]
Construction
The Gosset graph can be explicitly constructed as follows: the 56 vertices are the vectors in R8, obtained by permuting the coordinates and possibly taking the opposite of the vector (3, 3, −1, −1, −1, −1, −1, −1). Two such vectors are adjacent when their inner product is 8.
An alternative construction is based on the 8-vertex complete graph K8. The vertices of the Gosset graph can be identified with two copies of the set of edges of K8.
Two vertices of the Gosset graph that come from the same copy are adjacent if they correspond to disjoint edges of K8; two vertices that come from different copies are adjacent if they correspond to edges that share a single vertex.[2]
Properties
In the vector representation of the Gosset graph, two vertices are at distance two when their inner product is −8 and at distance three when their inner product is −24 (which is only possible if the vectors are each other's opposite). In the representation based on the edges of K8, two vertices of the Gosset graph are at distance three if and only if they correspond to different copies of the same edge of K8.
The Gosset graph is distance-regular with diameter three.[3]
The induced subgraph of the neighborhood of any vertex in the Gosset graph is isomorphic to the Schläfli graph.[3]
The automorphism group of the Gosset graph is isomorphic to the Coxeter group E7 and hence has order 2903040. The Gosset 321 polytope is a semiregular polytope. Therefore, the automorphism group of the Gosset graph, E7, acts transitively upon its vertices, making it a vertex-transitive graph.
The characteristic polynomial of the Gosset graph is[4]
Therefore, this graph is an integral graph.
References
2. ^{{citation | last = Haemers | first = Willem H. | doi = 10.1016/0024-3795(94)00166-9 | journal = Linear Algebra and its Applications | mr = 1375618 | pages = 265–278 | title = Distance-regularity and the spectrum of graphs | volume = 236 | year = 1996}}.
3. ^1 {{citation | last1 = Kabanov | first1 = V. V. | last2 = Makhnev | first2 = A. A. | last3 = Paduchikh | first3 = D. V. | doi = 10.1134/S1064562407030234 | issue = 5 | journal = Doklady Akademii Nauk | mr = 2451915 | pages = 583–586 | title = Characterization of some distance-regular graphs by forbidden subgraphs | volume = 414 | year = 2007}}.
4. ^{{citation | last1 = Brouwer | first1 = A. E. | last2 = Riebeek | first2 = R. J. | doi = 10.1023/A:1008670825910 | issue = 1 | journal = Journal of Algebraic Combinatorics | mr = 1635551 | pages = 15–28 | title = The spectra of Coxeter graphs | volume = 8 | year = 1998}}.
External links
- {{MathWorld|title=Gosset Graph|urlname=GossetGraph}}
- John Howe (Puritan)
- John Howes
- John Howland (Mayflower passenger)
- John Howlett (economist)
- John Howlett (political economist)
- John Howman
- John Hoyland (disambiguation)
- John Hoyland (writer)
- John Hoyles Boone
- John Hoyte
- John H. Panabaker
- John H. Parker
- John H. Piddington
- John H. Pitman High School
- John H. Raymond
- John H. Reagan High School
- John H. Robinson
- John H. Ross
- John H. Ross (WWII Pilot)
- John H. Ross (WWII pilot)
- John H. Rountree
- John H. Rubel
- John H. Rutherford
- John H. Sailhamer
- John H. Sampson