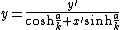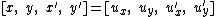“Gustav von Escherich”的意思、由来-开放百科全书

词条

Gustav von Escherich

释义

Biography
Work on hyperbolic geometry
References
External links

{{Infobox scientist
|name = Gustav Ritter von Escherich
|image =
|image_size =
|caption =
|birth_date = 1 June 1849
|birth_place = Mantua, Austrian Empire
|death_date = {{death date and age|1935|1|28|1849|6|1|df=y}}
|death_place = Vienna, Federal State of Austria
|residence = Austria
|citizenship = Austrian
|nationality =
|field = Mathematics
|work_institutions = University of Vienna
University of Graz
Graz University of Technology
|alma_mater = University of Vienna
(PhD, 1873)
|doctoral_advisor = Johannes Frischauf
Karl Friesach
|doctoral_students = Johann Radon
|known_for = Monatshefte für Mathematik und Physik
Austrian Mathematical Society
|prizes =
|footnotes =
|spouse =
|children =
}}

Gustav Ritter von Escherich (1 June 1849 – 28 January 1935) was an Austrian mathematician.

Biography

Born in Mantua, he studied mathematics and physics at the University of Vienna. From 1876 to 1879 he was professor at the University of Graz. In 1882 he went to the Graz University of Technology and in 1884 he went to the University of Vienna, where he also was president of the university in 1903/04.

Together with Emil Weyr he founded the journal Monatshefte für Mathematik und Physik and together with Ludwig Boltzmann and Emil Müller he founded the Austrian Mathematical Society.

Escherich died in Vienna.

Work on hyperbolic geometry

Following Eugenio Beltrami's (1868) discussion of hyperbolic geometry, Escherich in 1874 published a paper named "The geometry on surfaces of constant negative curvature". He used coordinates initially introduced by Christoph Gudermann (1830) for spherical geometry, which were adapted by Escherich using hyperbolic functions. For the case of translation of points on this surface of negative curvature, Escherich gave the following transformation on page 510:^[1]

and

which can be identified with the relativistic velocity addition formula by setting

and

or with a Lorentz boost by setting

.

These are in fact the relations between the coordinates of Gudermann/Escherich in terms of the Beltrami–Klein model and the Weierstrass coordinates of the hyperboloid model - this relation was pointed out by Homersham Cox (1882, p. 186),^[2] see History of Lorentz transformations#Escherich.

References

1. ^{{Cite journal|author=Escherich, G. von|year=1874|title=Die Geometrie auf den Flächen constanter negativer Krümmung|journal=Wiener Sitzungsberichte IIa|volume=69|pages=497-526|url=https://books.google.com/books?id=6e0DAAAAIAAJ&pg=PA497}}
2. ^{{Cite journal|author=Cox, H.|year=1881|title=Homogeneous coordinates in imaginary geometry and their application to systems of forces|journal=The quarterly journal of pure and applied mathematics|volume=18|issue=70|pages=178-192|url=http://resolver.sub.uni-goettingen.de/purl?PPN600494829_0018}}}

External links

{{MathGenealogy|id=27259}}

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。