“Haagerup property”的意思、由来-开放百科全书

词条

Haagerup property

释义

Definitions
Examples
Sources

In mathematics, the Haagerup property, named after Uffe Haagerup and also known as Gromov's a-T-menability, is a property of groups that is a strong negation of Kazhdan's property (T). Property (T) is considered a representation-theoretic form of rigidity, so the Haagerup property may be considered a form of strong nonrigidity; see below for details.

The Haagerup property is interesting to many fields of mathematics, including harmonic analysis, representation theory, operator K-theory, and geometric group theory.

Perhaps its most impressive consequence is that groups with the Haagerup Property satisfy the Baum–Connes conjecture and the related Novikov conjecture. Groups with the Haagerup property are also uniformly embeddable into a Hilbert space.

Definitions

Let be a second countable locally compact group. The following properties are all equivalent, and any of them may be taken to be definitions of the Haagerup property:

There is a proper continuous conditionally negative definite function .
has the Haagerup approximation property, also known as Property : there is a sequence of normalized continuous positive-definite functions 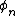which vanish at infinity on and converge to 1 uniformly on compact subsets of .
There is a strongly continuous unitary representation of which weakly contains the trivial representation and whose matrix coefficients vanish at infinity on .
There is a proper continuous affine isometric action of on a Hilbert space.

Examples

There are many examples of groups with the Haagerup property, most of which are geometric in origin. The list includes:

All compact groups (trivially). Note all compact groups also have property (T). The converse holds as well: if a group has both property (T) and the Haagerup property, then it is compact.
SO(n,1)
SU(n,1)
Groups acting properly on trees or on -trees
Coxeter groups
Amenable groups
Groups acting properly on CAT(0) cubical complexes

Sources

{{citation|MR=1852148 |last1= Cherix|first1= Pierre-Alain|last2= Cowling|first2= Michael|last3= Jolissaint|first3= Paul|last4= Julg|first4= Pierre|last5=Valette|first5= Alain|title= Groups with the Haagerup property. Gromov's a-T-menability.|series= Progress in Mathematics|volume= 197|publisher= Birkhäuser Verlag|place=Basel|year= 2001|isbn= 3-7643-6598-6|doi=10.1007/978-3-0348-8237-8 }}

2 : Representation theory|Geometric group theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。