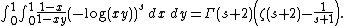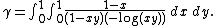“Hadjicostas's formula”的意思、由来-开放百科全书

词条

Hadjicostas's formula

释义

Statement
Background
Special cases
Notes
See also

In mathematics, Hadjicostas's formula is a formula relating a certain double integral to values of the Gamma function and the Riemann zeta function.

Statement

Let s be a complex number with s ≠ -1 and Re(s) > −2. Then

Here Γ is the Gamma function and ζ is the Riemann zeta function.

Background

The first instance of the formula was proved and used by Frits Beukers in his 1978 paper giving an alternative proof of Apéry's theorem.^[1] He proved the formula when s = 0, and proved an equivalent formulation for the case s = 1. This led Petros Hadjicostas to conjecture the above formula in 2004,^[2] and within a week it had been proven by Robin Chapman.^[3] He proved the formula holds when Re(s) > −1, and then extended the result by analytic continuation to get the full result.

Special cases

As well as the two cases used by Beukers to get alternate expressions for ζ(2) and ζ(3), the formula can be used to express the Euler-Mascheroni constant as a double integral by letting s tend to −1:

The latter formula was first discovered by Jonathan Sondow^[4] and is the one referred to in the title of Hadjicostas's paper.

Notes

1. ^{{cite journal|first1=F.|last1=Beukers|title=A note on the irrationality of ζ(2) and ζ(3)|journal=Bull. London Math. Soc.|volume=11|issue=3|year=1979 |pages=268–272|doi=10.1112/blms/11.3.268}}
2. ^{{cite arXiv|first1=P.|last1=Hadjicostas|eprint=math.NT/0405423|title=A conjecture-generalization of Sondow’s formula|year=2004}}
3. ^{{cite arXiv|first1=R.|last1=Chapman|eprint=math/0405478|title=A proof of Hadjicostas’s conjecture|year=2004}}
4. ^{{cite journal|first1=J.|last1=Sondow|title=Criteria for irrationality of Euler's constant|journal=Proc. Amer. Math. Soc.|volume=131|year=2003|pages= 3335–3344|doi=10.1090/S0002-9939-03-07081-3 }}

Statement

Background

Special cases

Notes

See also