1. Proof Outline

2. See also

3. Notes

4. Further reading

The Hammersley–Clifford theorem is a result in probability theory, mathematical statistics and statistical mechanics, that gives necessary and sufficient conditions under which a strictly positive probability distribution{{what|reason=This is completely underspecified!! A probability distribution *on what*? Without specifying the graph, lattice, state, process, or other underlying structure where the "randomness" is occuring, the definition makes little sense.|date=April 2016}} can be represented as a Markov network (also known as a Markov random field). It is the fundamental theorem of random fields.^[1] It states that a probability distribution that has a strictly positive mass or density satisfies one of the Markov properties with respect to an undirected graph G if and only if it is a Gibbs random field, that is, its density can be factorized over the cliques (or complete subgraphs) of the graph.

The relationship between Markov and Gibbs random fields was initiated by Roland Dobrushin^[2] and Frank Spitzer^[3] in the context of statistical mechanics. The theorem is named after John Hammersley and Peter Clifford who proved the equivalence in an unpublished paper in 1971.^[4][5] Simpler proofs using the inclusion–exclusion principle were given independently by Geoffrey Grimmett,^[6] Preston^[7] and Sherman^[8] in 1973, with a further proof by Julian Besag in 1974.^[9]

Proof Outline

It is a trivial matter to show that a Gibbs random field satisfies every Markov property. As an example of this fact, see the following:

In the image to the right, a Gibbs random field over the provided graph has the form . If variables and are fixed, then the global Markov property requires that: 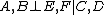(see conditional independence), since forms a barrier between and .

With and constant, 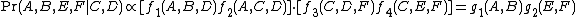where and 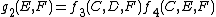. This implies that .

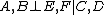To establish that every positive probability distribution that satisfies the local Markov property is also a Gibbs random field, the following lemma, which provides a means for combining different factorizations, needs to be proven:

Let denote the set of all random variables under consideration, and let and denote arbitrary sets of variables. (Here, given an arbitrary set of variables , will also denote an arbitrary assignment to the variables from .)

If

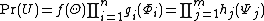
for functions and 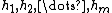, then there exist functions and such that

In other words, provides a template for further factorization of .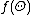

Let 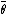be an arbitrary assignment to the variables from . For an arbitrary set of variables , let denote the assignment 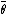restricted to the variables from . It is then the case that

Let

and

for each 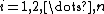so

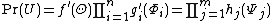
hence

Since ,

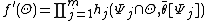
Letting

finally gives:

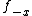Lemma 1 provides a means of combining two different factorizations of . The local Markov property implies that for any random variable , that there exists factors and such that:

where are the neighbors of node . Applying Lemma 1 repeatedly eventually factors into a product of clique potentials (see the image on the right).

See also

• Markov random field
• Conditional random field

Notes

Further reading

• {{citation|first=Jeff |last=Bilmes|url=http://ssli.ee.washington.edu/courses/ee512/handout2.pdf|title=Handout 2: Hammersley–Clifford|date=Spring 2006}}, course notes from University of Washington course.
• {{citation|last=Grimmett|first=Geoffrey|title=Probability on Graphs, Chapter 7|url=http://www.statslab.cam.ac.uk/~grg/books/pgs.html}}
• {{citation|last=Langseth|first=Helge|title=The Hammersley–Clifford Theorem and its Impact on Modern Statistics|url=http://www.idi.ntnu.no/~helgel/thesis/forelesning.pdf}}

• Xalaftala
• Xalala Dam
• Xalalá Dam
• Xalalá hydroelectric dam
• Xalanc
• Xalapa Cathedral
• Xalapa Enriquez
• Xalapa-Enriquez
• Xalapa Museum of Anthropology
• Xalapa, Ver.
• Xalapa, Veracruz
• Xalapeños
• Xalatala
• Xalatalabina
• Xalatalabine
• Xalatalabinə
• Xalatan Fixed Flow Device
• Xalatlaco
• Xalbal River
• Xaldan
• Xalfahonu
• Xalfakuca
• Xalfalar
• Xalfalar, Davachi
• Xalfalar, Masally