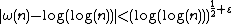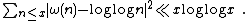“Hardy–Ramanujan theorem”的意思、由来-开放百科全书

词条

Hardy–Ramanujan theorem

释义

Precise statement
History
Generalizations
References

In mathematics, the Hardy–Ramanujan theorem, proved by {{harvs|txt|last1=Hardy|first1=G. H. |authorlink1=G. H. Hardy|last2=Ramanujan|first2=Srinivasa|authorlink2=Srinivasa Ramanujan|year=1917}}, states that the normal order of the number ω(n) of distinct prime factors of a number n is log(log(n)).

Roughly speaking, this means that most numbers have about this number of distinct prime factors.

Precise statement

A more precise version states that for any real-valued function ψ(n) that tends to infinity as n tends to infinity

or more traditionally

for almost all (all but an infinitesimal proportion of) integers. That is, let g(x) be the number of positive integers n less than x for which the above inequality fails: then g(x)/x converges to zero as x goes to infinity.

History

A simple proof to the result {{harvtxt|Turán|1934}} was given by Pál Turán, who used the Turán sieve to prove that

Generalizations

The same results are true of Ω(n), the number of prime factors of n counted with multiplicity.

This theorem is generalized by the Erdős–Kac theorem, which shows that ω(n) is essentially normally distributed.

References

{{citation|first=G. H.|last= Hardy| authorlink=G. H. Hardy| first2= S.|last2=Ramanujan| authorlink2=Srinivasa Ramanujan |title=The normal number of prime factors of a number n| journal= Quarterly Journal of Mathematics |volume= 48 |year=1917|pages= 76–92 | url=http://www.imsc.res.in/~rao/ramanujan/CamUnivCpapers/Cpaper35/page1.htm | jfm=46.0262.03 }}
{{citation | last1=Kuo | first1=Wentang | last2=Liu | first2=Yu-Ru | chapter=The Erdős–Kac theorem and its generalizations | pages=209–216 | editor1-last=De Koninck | editor1-first=Jean-Marie | editor1-link=Jean-Marie De Koninck | editor2-last=Granville | editor2-first=Andrew | editor2-link=Andrew Granville | editor3-last=Luca | editor3-first=Florian | title=Anatomy of integers. Based on the CRM workshop, Montreal, Canada, March 13--17, 2006 | location=Providence, RI | publisher=American Mathematical Society | series=CRM Proceedings and Lecture Notes | volume=46 | year=2008 | isbn=978-0-8218-4406-9 | zbl=1187.11024 }}
{{citation | last=Turán | first=Pál | authorlink=Pál Turán | title=On a theorem of Hardy and Ramanujan | journal=Journal of the London Mathematical Society | volume=9 | pages=274–276 | year=1934 | issn=0024-6107 | zbl=0010.10401 | doi = 10.1112/jlms/s1-9.4.274 }}
{{springer|id=H/h110080|first=A.|last= Hildebrand}}

2 : Theorems in analytic number theory|Theorems about prime numbers

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。