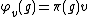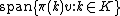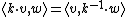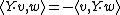- Definition
- Notes
- References
- See also
In mathematics, specifically in the representation theory of Lie groups, a Harish-Chandra module, named after the Indian mathematician and physicist Harish-Chandra, is a representation of a real Lie group, associated to a general representation, with regularity and finiteness conditions. When the associated representation is a 
-module, then its Harish-Chandra module is a representation with desirable factorization properties.
Definition
Let G be a Lie group and K a compact subgroup of G. If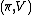 
is a representation of G, then the Harish-Chandra module of 
is the subspace X of V consisting of the K-finite smooth vectors in V. This means that X includes exactly those vectors v such that the map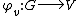 
via
is smooth, and the subspace
is finite-dimensional.
Notes
In 1973, Lepowsky showed that any irreducible -module X is isomorphic to the Harish-Chandra module of an irreducible representation of G on a Hilbert space. Such representations are admissible, meaning that they decompose in a manner analogous to the prime factorization of integers. (Of course, the decomposition may have infinitely many distinct factors!) Further, a result of Harish-Chandra indicates that if G is a reductive Lie group with maximal compact subgroup K, and X is an irreducible
-module with a positive definite Hermitian form satisfying
and
for all 
and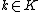 
, then X is the Harish-Chandra module of a unique irreducible unitary representation of G.
References
- {{Citation
| last=Vogan, Jr.
| first=David A.
| title=Unitary Representations of Reductive Lie Groups
| year=1987
| publisher=Princeton University Press
| series=Annals of Mathematics Studies
| volume=118
| isbn=978-0-691-08482-4
}}
See also
- (g,K)-module
- Admissible representation
- Unitary representation