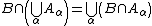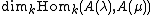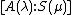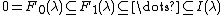- Examples
- Notes
- References
- See also
In the mathematical field of representation theory, a highest-weight category is a k-linear category C (here k is a field) that
- is locally artinian[1]
- has enough injectives
- satisfies
for all subobjects B and each family of subobjects {Aα} of each object X
and such that there is a locally finite poset Λ (whose elements are called the weights of C) that satisfies the following conditions:[2]
- The poset Λ indexes an exhaustive set of non-isomorphic simple objects {S(λ)} in C.
- Λ also indexes a collection of objects {A(λ)} of objects of C such that there exist embeddings S(λ) → A(λ) such that all composition factors S(μ) of A(λ)/S(λ) satisfy μ < λ.[3]
- For all μ, λ in Λ,
is finite, and the multiplicity[4]
is also finite.
- Each S(λ) has an injective envelope I(λ) in C equipped with an increasing filtration
such that
-
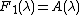
- for n > 1,
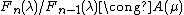 for some μ = μ(n) > λ
for some μ = μ(n) > λ - for each μ in Λ, μ(n) = μ for only finitely many n
-
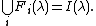
Examples
- The module category of the
 -algebra of upper triangular
-algebra of upper triangular  matrices over
matrices over  .
. - This concept is named after the category of highest-weight modules of Lie-algebras.
- A finite-dimensional
 -algebra
-algebra  is quasi-hereditary iff its module category is a highest-weight category. In particular all module-categories over semisimple and hereditary algebras are highest-weight categories.
is quasi-hereditary iff its module category is a highest-weight category. In particular all module-categories over semisimple and hereditary algebras are highest-weight categories. - A cellular algebra over a field is quasi-hereditary (and hence its module category a highest-weight category) iff its Cartan-determinant is 1.
Notes
1. ^In the sense that it admits arbitrary direct limits of subobjects and every object is a union of its subobjects of finite length.
2. ^{{harvnb|Cline|Scott|1988|loc=§3}}
3. ^Here, a composition factor of an object A in C is, by definition, a composition factor of one of its finite length subobjects.
4. ^Here, if A is an object in C and S is a simple object in C, the multiplicity [A:S] is, by definition, the supremum of the multiplicity of S in all finite length subobjects of A.
2. ^{{harvnb|Cline|Scott|1988|loc=§3}}
3. ^Here, a composition factor of an object A in C is, by definition, a composition factor of one of its finite length subobjects.
4. ^Here, if A is an object in C and S is a simple object in C, the multiplicity [A:S] is, by definition, the supremum of the multiplicity of S in all finite length subobjects of A.
References
- {{cite journal
| last1 = Cline
| first1 = E.
| last2 = Parshall
| first2 = B.
| last3 = Scott
| first3 = L.
|date=January 1988
| title = Finite-dimensional algebras and highest-weight categories
| journal = Journal für die reine und angewandte Mathematik
| volume = 1988
| issue = 391
| pages = 85–99
| location = Berlin, Germany
| publisher = Walter de Gruyter
| format = pdf
| issn = 0075-4102
| oclc = 1782270
| doi = 10.1515/crll.1988.391.85
| citeseerx = 10.1.1.112.6181
| url = http://u.math.biu.ac.il/~margolis/Representation%20Theory%20Seminar/Highest%20Weight%20Categories.pdf
| accessdate=2012-07-17
See also
- Category O
1 : Representation theory
- Social imperialisms
- Social imperialist
- Social-imperialistic
- Social imperialistic
- Social-imperialists
- Social imperialists
- Social implications of the Filipino domestic helper (Canada)
- Social Implications of the Filipino Domestic Helper (in Canada)
- Social Inclusion, Participative Democracy and Human Rights
- Social influence of Gangnam Style
- Social informational influence
- Social information architecture
- Social Information Architecture
- Social-information processing
- Social Information Processing (Cognition)
- Social information processing (disambiguation)
- Social information processing theory
- Social information processing (Theory)
- Social Insurance and Allied Services
- Social Insurance Fund of the Russian Federation
- Social interaction and first-person shooters
- Social interactions and first-person shooters
- Social Intercourse
- Social Intercourse (album)
- Social interpretations of race