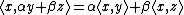“Hilbert C*-module”的意思、由来-开放百科全书

Hilbert C*-modules are mathematical objects which generalise the notion of a Hilbert space (which itself is a generalisation of Euclidean space), in that they endow a linear space with an "inner product" which takes values in a C*-algebra. Hilbert C*-modules were first introduced in the work of Irving Kaplansky in 1953, which developed the theory for commutative, unital algebras (though Kaplansky observed that the assumption of a unit element was not "vital").^[1] In the 1970s the theory was extended to non-commutative C*-algebras independently by William Lindall Paschke^[2] and Marc Rieffel, the latter in a paper which used Hilbert C*-modules to construct a theory of induced representations of C*-algebras.^[3] Hilbert C*-modules are crucial to Kasparov's formulation of KK-theory,^[4] and provide the right framework to extend the notion of Morita equivalence to C*-algebras.^[5] They can be viewed as the generalization of vector bundles to noncommutative C*-algebras and as such play an important role in noncommutative geometry, notably in C*-algebraic quantum group theory,^[6]^[7] and groupoid C*-algebras.

Definitions

Inner-product A-modules

Let A be a C*-algebra (not assumed to be commutative or unital), its involution denoted by *. An inner-product A-module (or pre-Hilbert A-module) is a complex linear space E which is equipped with a compatible right A-module structure, together with a map

Hilbert A-modules

An analogue to the Cauchy–Schwarz inequality holds for an inner-product A-module E:^[10]

The norm-completion of E, still denoted by E, is said to be a Hilbert A-module or a Hilbert C*-module over the C*-algebra A.

The Cauchy–Schwarz inequality implies the inner product is jointly continuous in norm and can therefore be extended to the completion.

Similarly, if {e_λ} is an approximate unit for A (a net of self-adjoint elements of A for which ae_λ and e_λa tend to a for each a in A), then for x in E

then the closure of <E,E> is a two-sided ideal in A. Two-sided ideals are C*-subalgebras and therefore possess approximate units. One can verify that E<E,E> is dense in E. In the case when <E,E> is dense in A, E is said to be full. This does not generally hold.

Examples

Hilbert spaces

A complex Hilbert space H is a Hilbert C-module under its inner product, the complex numbers being a C*-algebra with an involution given by complex conjugation.

Vector bundles

If X is a locally compact Hausdorff space and E a vector bundle over X with a Riemannian metric g, then the space of continuous sections of E is a Hilbert C(X)-module. The inner product is given by

The converse holds as well: Every countably generated Hilbert C*-module over a commutative C*-algebra A = C(X) is isomorphic to the space of sections vanishing at infinity of a continuous field of Hilbert spaces over X.

C*-algebras

Any C*-algebra A is a Hilbert A-module under the inner product <a,b> = a*b. By the C*-identity, the Hilbert module norm coincides with C*-norm on A.

One may also consider the following subspace of elements in the countable direct product of A

Endowed with the obvious inner product (analogous to that of Aⁿ), the resulting Hilbert A-module is called the standard Hilbert module.

See also

Notes

1. ^{{cite journal| last = Kaplansky| first = I.| authorlink = Irving Kaplansky| title = Modules over operator algebras| journal = American Journal of Mathematics| volume = 75| issue = 4| pages = 839–853| year = 1953| doi = 10.2307/2372552| jstor = 2372552}}
2. ^{{cite journal| last = Paschke| first = W. L.| title = Inner product modules over B*-algebras| journal = Transactions of the American Mathematical Society| volume = 182| pages = 443–468| year = 1973| doi = 10.2307/1996542| jstor = 1996542}}
3. ^{{cite journal| last = Rieffel| first = M. A.| title = Induced representations of C*-algebras| journal = Advances in Mathematics| volume = 13| pages = 176–257| publisher = Elsevier| year = 1974| doi = 10.1016/0001-8708(74)90068-1| issue = 2}}
4. ^{{cite journal| last = Kasparov| first = G. G.| title = Hilbert C*-modules: Theorems of Stinespring and Voiculescu| journal = Journal of Operator Theory| volume = 4| pages = 133–150| publisher = Theta Foundation| year = 1980}}
5. ^{{cite journal| last = Rieffel| first = M. A.| title = Morita equivalence for operator algebras| journal = Proceedings of Symposia in Pure Mathematics| volume = 38| pages = 176–257| publisher = American Mathematical Society| year = 1982}}
6. ^{{cite journal| last = Baaj| first = S.|author2=Skandalis, G.| title = Unitaires multiplicatifs et dualité pour les produits croisés de C*-algèbres| journal = Annales Scientifiques de l'École Normale Supérieure| volume = 26| issue = 4| pages = 425–488| year = 1993}}
7. ^{{cite journal| last = Woronowicz| first = S. L.| authorlink = S. L. Woronowicz| title = Unbounded elements affiliated with C*-algebras and non-compact quantum groups| journal = Communications in Mathematical Physics| volume = 136| pages = 399–432| year = 1991| doi = 10.1007/BF02100032|bibcode = 1991CMaPh.136..399W| issue = 2 }}
8. ^{{cite book| last = Arveson| first = William| authorlink = William Arveson|title = An Invitation to C*-Algebras| publisher = Springer-Verlag| year = 1976| page = 35}}
9. ^In the case when A is non-unital, the spectrum of an element is calculated in the C*-algebra generated by adjoining a unit to A.
10. ^This result in fact holds for semi-inner-product A-modules, which may have non-zero elements x such that <x,x> = 0, as the proof does not rely on the nondegeneracy property.