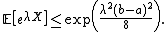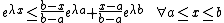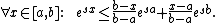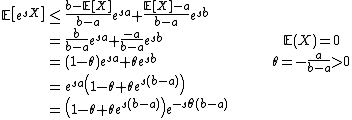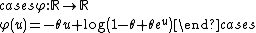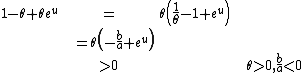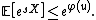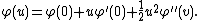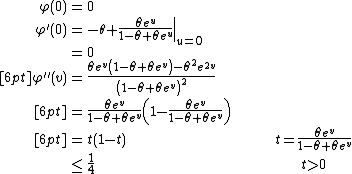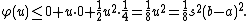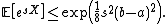“Hoeffding's lemma”的意思、由来-开放百科全书

词条

Hoeffding's lemma

释义

Statement of the lemma
A brief proof of the lemma
More detailed proof
See also
Notes

In probability theory, Hoeffding's lemma is an inequality that bounds the moment-generating function of any bounded random variable.^[1] It is named after the Finnish–American mathematical statistician Wassily Hoeffding.

The proof of Hoeffding's lemma uses Taylor's theorem and Jensen's inequality. Hoeffding's lemma is itself used in the proof of McDiarmid's inequality.

Statement of the lemma

Let X be any real-valued random variable with expected value 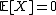and such that 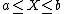almost surely. Then, for all ,

Note that because of the assumption that the random variable has zero expectation, the and in the lemma must satisfy .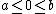

A brief proof of the lemma

Since 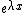is a convex function of , we have

So,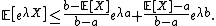

Let 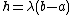, 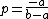and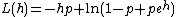

Then, 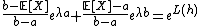since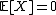

Taking derivative of ,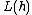

for all h.

By Taylor's expansion,

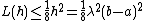
Hence,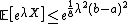

(The proof below is the same proof with more explanation.)

More detailed proof

First note that if one of or is zero, then 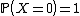and the inequality follows. If both are nonzero, then must be negative and must be positive.

Next, recall that 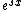is a convex function on the real line:

Applying to both sides of the above inequality gives us:

Let 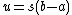and define:

is well defined on , to see this we calculate:

The definition of implies

By Taylor's theorem, for every real there exists a between and such that

Note that:

Therefore,

This implies

Notes

1. ^{{cite book|author=Pascal Massart|title=Concentration Inequalities and Model Selection: Ecole d'Eté de Probabilités de Saint-Flour XXXIII - 2003|url=https://books.google.com/books?id=ZI67BQAAQBAJ&pg=PA21|date=26 April 2007|publisher=Springer|isbn=978-3-540-48503-2|page=21}}

1 : Probabilistic inequalities

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Statement of the lemma

A brief proof of the lemma

More detailed proof

See also

Notes