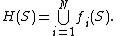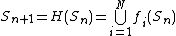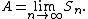“Hutchinson operator”的意思、由来-开放百科全书

词条

Hutchinson operator

释义

Definition
Properties
References

In mathematics, in the study of fractals, a Hutchinson operator^[1] is the collective action of a set of contractions, called an iterated function system.^[2] The iteration of the operator converges to a unique attractor, which is the often self-similar fixed set of the operator.

Definition

Let 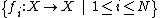be an iterated function system, or a set of contractions from a compact set to itself. The operator is defined over subset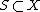s as

A key question is to describe the attractors 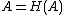of this operator, which are compact sets. One way of generating such a set is to start with an initial compact set 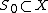(which can be a single point, called a seed) and iterate as follows

and taking the limit, the iteration converges to the attractor

Properties

Hutchinson showed in 1981 the existence and uniqueness of the attractor . The proof follows by showing that the Hutchinson operator is contractive on the set of compact subsets of in the Hausdorff distance.

The collection of functions together with composition form a monoid. With N functions, then one may visualize the monoid as a full N-ary tree or a Cayley tree.

References

1. ^{{cite journal | last=Hutchinson | first=John E. | title=Fractals and self similarity | journal=Indiana Univ. Math. J. | volume=30 | year=1981 | pages=713–747 | doi=10.1512/iumj.1981.30.30055 | issue=5 }}
2. ^{{cite journal | last=Barnsley | first=Michael F. | author2=Stephen Demko | title=Iterated function systems and the global construction of fractals | journal=Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences | volume=399 | year=1985 | pages=243–275 | issue=1817 }}

1 : Fractals

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。