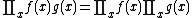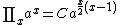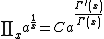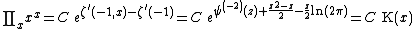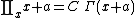- Period rule
- Connection to indefinite sum
- Alternative usage
- Rules
- List of indefinite products
- See also
- References
- Further reading
- External links
In mathematics, the indefinite product operator is the inverse operator of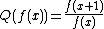 
. It is a discrete version of the geometric integral of geometric calculus, one of the non-Newtonian calculi. Some authors use term discrete multiplicative integration[1]
Thus
More explicitly, if 
, then
If F(x) is a solution of this functional equation for a given f(x), then so is CF(x) for any constant C. Therefore, each indefinite product actually represents a family of functions, differing by a multiplicative constant.
Period rule
If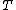 
is a period of function 
then
Connection to indefinite sum
Indefinite product can be expressed in terms of indefinite sum:
Alternative usage
Some authors use the phrase "indefinite product" in a slightly different but related way to describe a product in which the numerical value of the upper limit is not given.[2] e.g.
.
Rules
List of indefinite products
This is a list of indefinite products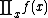 
. Not all functions have an indefinite product which can be expressed in elementary functions.
(see K-function)
(see Barnes G-function)
(see super-exponential function)
See also
- Indefinite sum
- Product integral
- List of derivatives and integrals in alternative calculi
- Multiplicative calculus
- Fractal derivative
References
2. ^Algorithms for Nonlinear Higher Order Difference Equations, Manuel Kauers
Further reading
- http://reference.wolfram.com/mathematica/ref/Product.html -Indefinite products with Mathematica
- http://www.math.rwth-aachen.de/MapleAnswers/660.html{{dead link|date=November 2017 |bot=InternetArchiveBot |fix-attempted=yes }} - bug in Maple V to Maple 8 handling of indefinite product
- [https://web.archive.org/web/20110617053801/http://www.math.tu-berlin.de/~mueller/HowToAdd.pdf Markus Müller. How to Add a Non-Integer Number of Terms, and How to Produce Unusual Infinite Summations]
- [https://arxiv.org/abs/math/0502109 Markus Mueller, Dierk Schleicher. Fractional Sums and Euler-like Identities]
External links
- [https://sites.google.com/site/nonnewtoniancalculus/ Non-Newtonian calculus website]
- Waitan Bridge station
- Waitan Bridge Station
- Wai T'an Customs Building
- Wait and Return EP
- Waitangitahuna River
- Waitangitāhuna River
- Waitangi Upper Marae
- Waitara Bears
- Waitard
- Waita Setu
- Wait Block
- WaitButWhy
- Wait But Why
- @waitbutwhy
- Wait by the River
- Wait Calculation
- Wait calculation
- Wait (Chantel Jeffries song)
- Waite, Anthony
- Wai-te-ata Music Press
- Waite, Byron Sylvester
- Waite, Charles
- Waite-Colman Smith deck
- Waite, David
- Waited To Exhale