“Index set (recursion theory)”的意思、由来-开放百科全书

词条

Index set (recursion theory)

释义

Definition
Index sets and Rice's theorem
Notes
References

In the field of recursion theory, index sets describe classes of partial recursive functions, specifically they give all indices of functions in that class according to a fixed enumeration of partial recursive functions (a Gödel numbering).

Definition

Fix an enumeration of all partial recursive functions, or equivalently of recursively enumerable sets whereby the eth such set is and the eth such function (whose domain is ) is .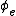

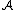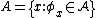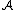Let be a class of partial recursive functions. If then is the index set of . In general is an index set if for every 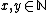with 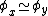(i.e. they index the same function), we have 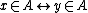. Intuitively, these are the sets of natural numbers that we describe only with reference to the functions they index.

Index sets and Rice's theorem

Most index sets are incomputable (non-recursive) aside from two trivial exceptions. This is stated in Rice's theorem:

Let be a class of partial recursive functions with index set . Then is recursive if and only if is empty, or is all of .

where 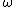is the set of natural numbers, including zero.

Rice's theorem says "any nontrivial property of partial recursive functions is undecidable"^[1]

Notes

1. ^{{cite book | title=Classical Recursion Theory, Volume 1| author=Odifreddi, P. G. }}; page 151

References

{{cite book | title=Classical Recursion Theory, Volume 1| author=Odifreddi, P. G. | publisher=Elsevier| year=1992 | isbn=0-444-89483-7 | pages=668 }}
{{ cite book | title=Theory of Recursive Functions and Effective Computability | author=Rogers Jr., Hartley | publisher=MIT Press|isbn=0-262-68052-1 | pages=482 | year=1987}}

1 : Computability theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。