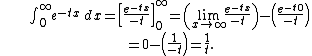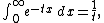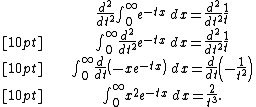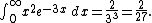- Example
In mathematics, integration by parametric derivatives is a method of integrating certain functions.
Example
For example, suppose we want to find the integral
Since this is a product of two functions that are simple to integrate separately, repeated integration by parts is certainly one way to evaluate it. However, we may also evaluate this by starting with a simpler integral and an added parameter, which in this case is t = 3:
This converges only for t > 0, which is true of the desired integral. Now that we know
we can differentiate both sides twice with respect to t (not x) in order to add the factor of x2 in the original integral.
This is the same form as the desired integral, where t = 3. Substituting that into the above equation gives the value:
{{mathanalysis-stub}}
1 : Integral calculus
- 2005 Wimbledon Championships - Men's Doubles Qualifying
- 2005 Wimbledon Championships - Men's Singles Qualifying
- 2005 Wimbledon Championships - Wheelchair Men's Doubles
- 2005 Wimbledon Championships - Women's Doubles Qualifying
- 2005 Wimbledon Championships - Women's Singles Qualifying
- 2005 Wimbledon Championships – Boys' Doubles
- 2005 Wimbledon Championships – Boys' Singles
- 2005 Wimbledon Championships – Girls' Doubles
- 2005 Wimbledon Championships – Men's Doubles Qualifying
- 2005 Wimbledon Championships – Wheelchair Men's Doubles
- 2005 Wimbledon Championships – Women's Doubles Qualifying
- 2005 Winthrop Eagles men's soccer team
- 2005 Wisconsin Badgers football
- 2005 Wisconsin Badgers football season
- 2005 Wismilak International - Doubles
- 2005 Wismilak International - Singles
- 2005 Wismilak International – Doubles
- 2005 W-League
- 2005 Women's Cricket World Cup squads
- 2005 Women's EuroHockey Nations Championship
- 2005 Women's Futsal Islamic Games
- 2005 Women's Hockey European Championship
- 2005 Women's Hockey European Nations Cup
- 2005 Women's Hockey Junior World Cup
- 2005 Women's Lacrosse World Cup